ເນື້ອຫາ

• ຂັ້ນຕອນ
• ສ່ວນທີ 1 ຂອງ 2: ການຊອກຫາປັດໃຈຫຼັກ
• ສ່ວນທີ 2 ຂອງ 2: ການ ນຳ ໃຊ້ປັດໃຈຫຼັກ
• ຕົວຢ່າງຂອງ ໜ້າ ວຽກ
• ຄໍາແນະນໍາ
• ຄຳ ເຕືອນ

ຕົວເລກ ທຳ ມະຊາດໃດກໍ່ຕາມສາມາດຖືກເນົ່າເປື່ອຍລົງເປັນຜະລິດຕະພັນຂອງປັດໃຈຕົ້ນຕໍ. ຖ້າເຈົ້າບໍ່ມັກການຈັດການກັບຕົວເລກໃຫຍ່ເຊັ່ນ: 5733, ຮຽນຮູ້ວິທີການປັດໄຈພວກມັນ (ໃນກໍລະນີນີ້, 3 x 3 x 7 x 7 x 13). ວຽກງານທີ່ຄ້າຍຄືກັນແມ່ນພົບເລື້ອຍ often ຢູ່ໃນການເຂົ້າລະຫັດລັບ, ເຊິ່ງຈັດການກັບບັນຫາຄວາມປອດໄພດ້ານຂໍ້ມູນຂ່າວສານ. ຖ້າເຈົ້າຍັງບໍ່ພ້ອມສ້າງລະບົບອີເມລທີ່ປອດໄພຂອງເຈົ້າເອງເທື່ອ, ຮຽນຮູ້ວິທີການຄິດໄລ່ຕົວເລກກ່ອນ.

ຂັ້ນຕອນ

ສ່ວນທີ 1 ຂອງ 2: ການຊອກຫາປັດໃຈຫຼັກ

1. 1 ຮຽນຮູ້ວ່າປັດໃຈແມ່ນຫຍັງ. ການເສື່ອມສະພາບຂອງຕົວເລກໃດ ໜຶ່ງ ເຂົ້າໄປໃນຜົນຂອງປັດໃຈແມ່ນຂະບວນການ "ແຍກ" ມັນອອກເປັນສ່ວນນ້ອຍ smaller.ເມື່ອຄູນ, ສ່ວນເຫຼົ່ານີ້, ຫຼືປັດໃຈ, ໃຫ້ຕົວເລກເດີມ.
   • ຕົວຢ່າງ, 18າຍເລກ 18 ສາມາດຍ່ອຍສະຫຼາຍໄດ້ເປັນຜະລິດຕະພັນຕໍ່ໄປນີ້: 1 x 18, 2 x 9, ຫຼື 3 x 6.
2. 2 ຈື່ໄວ້ວ່າຕົວເລກ ສຳ ຄັນແມ່ນຫຍັງ. ຕົວເລກ ໜຶ່ງ ສາມາດຫານໄດ້ດ້ວຍຕົວເລກສອງຕົວໂດຍບໍ່ມີຕົວເລກ: ຕົວຂອງມັນເອງແລະໂດຍ 1. ຕົວຢ່າງ, ຕົວເລກ 5 ສາມາດເປັນຕົວແທນເປັນຜົນໄດ້ຮັບຂອງ 5 ແລະ 1. ຕົວເລກນີ້ບໍ່ສາມາດຍ່ອຍສະຫລາຍໄປເປັນປັດໃຈອື່ນໄດ້. ຈຸດປະສົງຂອງການແຍກຕົວເລກເຂົ້າໄປໃນບັນດາປັດໃຈຫຼັກແມ່ນເພື່ອສະແດງວ່າມັນເປັນຜົນຜະລິດຂອງຕົວເລກຊັ້ນນໍາ. ອັນນີ້ເປັນປະໂຫຍດໂດຍສະເພາະເມື່ອປະຕິບັດກັບເສດສ່ວນ, ເພາະມັນຊ່ວຍໃຫ້ເຈົ້າສາມາດປຽບທຽບແລະເຮັດໃຫ້ພວກມັນງ່າຍຂຶ້ນ.
3. 3 ເລີ່ມຕົ້ນດ້ວຍຕົວເລກເດີມ. ເລືອກຕົວເລກປະສົມທີ່ຫຼາຍກວ່າ 3. ມັນບໍ່ມີຄວາມາຍຫຍັງທີ່ຈະເອົາຕົວເລກຫຼັກ, ເພາະວ່າມັນສາມາດແບ່ງໄດ້ດ້ວຍຕົວມັນເອງແລະຕົວເລກດຽວເທົ່ານັ້ນ.
   • ຕົວຢ່າງ: ພວກເຮົາເນົ່າເປື່ອຍໃຫ້numberາຍເລກ 24 ກາຍເປັນຜົນຄູນຂອງຕົວເລກ ທຳ ອິດ.
4. 4 ໃຫ້ແບ່ງຕົວເລກນີ້ເປັນຜົນໄດ້ຮັບຂອງສອງປັດໃຈ. ຊອກຫາຕົວເລກສອງຕົວທີ່ມີຜະລິດຕະພັນເທົ່າກັບຕົວເລກເດີມ. ສາມາດໃຊ້ປັດໃຈອັນໃດກໍ່ໄດ້, ແຕ່ມັນງ່າຍທີ່ຈະເອົາຕົວເລກຫຼັກ. ວິທີທີ່ດີອັນ ໜຶ່ງ ແມ່ນພະຍາຍາມຫານຕົວເລກດັ້ງເດີມກ່ອນ 2, ຈາກນັ້ນ 3, ຈາກນັ້ນ 5, ແລະກວດເບິ່ງວ່າຕົວເລກໃດທີ່ມັນແບ່ງອອກໂດຍບໍ່ມີສ່ວນທີ່ເຫຼືອ.
   • ຕົວຢ່າງ: ຖ້າເຈົ້າບໍ່ຮູ້ປັດໃຈຂອງ 24, ໃຫ້ພະຍາຍາມຫານມັນດ້ວຍຕົວນ້ອຍ. ດັ່ງນັ້ນເຈົ້າຈະພົບວ່າຕົວເລກທີ່ໄດ້ຮັບນັ້ນແມ່ນແບ່ງອອກໂດຍ 2: 24 = 2 x 12... ນີ້ເປັນການເລີ່ມຕົ້ນທີ່ດີ.
   • ເນື່ອງຈາກວ່າ 2 ເປັນຕົວເລກຕົ້ນຕໍ, ມັນເປັນການດີທີ່ຈະໃຊ້ມັນເມື່ອແຍກຕົວເລກອອກເປັນເລກ.
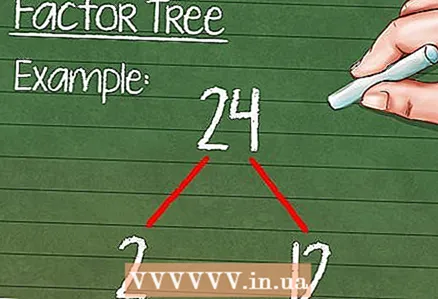5. 5 ເລີ່ມສ້າງຕົ້ນໄມ້ຄູນ. ຂັ້ນຕອນງ່າຍ simple ນີ້ຈະຊ່ວຍໃຫ້ເຈົ້າຄິດໄລ່ເລກໄດ້. ເພື່ອເລີ່ມຕົ້ນດ້ວຍ, ແຕ້ມສອງ "ສາຂາ" ລົງຈາກຕົວເລກເດີມ. ໃນຕອນທ້າຍຂອງແຕ່ລະສາຂາ, ໃຫ້ຂຽນປັດໃຈທີ່ພົບ.
   • ຕົວຢ່າງ:
   •    24
   •     /
   • 2    12
6. 6 ປັດໄຈແຖວຕໍ່ໄປຂອງຕົວເລກ. ເບິ່ງຕົວເລກໃtwo່ສອງຕົວ (ແຖວທີສອງຂອງຕົ້ນຄູນ). ເຂົາເຈົ້າທັງສອງເປັນຕົວເລກຫຼັກບໍ? ຖ້າອັນໃດອັນນຶ່ງບໍ່ງ່າຍດາຍ, ໃຫ້ປັດໄຈມັນດ້ວຍສອງປັດໃຈ. ເຮັດໃຫ້ອີກສອງສາຂາແລະຂຽນສອງປັດໃຈໃin່ໃສ່ໃນແຖວທີສາມຂອງຕົ້ນໄມ້.
   • ຕົວຢ່າງ: 12 ບໍ່ແມ່ນຕົວເລກ ສຳ ຄັນ, ສະນັ້ນມັນຄວນຈະຖືກຄິດໄລ່ດ້ວຍປັດໃຈ. ໃຊ້ຕົວເນົ່າເປື່ອຍ 12 = 2 x 6 ແລະຂຽນມັນໃສ່ແຖວທີສາມຂອງຕົ້ນໄມ້:
   •    24
   •     /
   • 2   12
   •        /
   • 2 x 6
7. 7 ສືບຕໍ່ລົງຕົ້ນໄມ້. ຖ້າ ໜຶ່ງ ໃນປັດໃຈໃturns່ກາຍເປັນຕົວເລກທີ່ ສຳ ຄັນ, ແຕ້ມ ໜຶ່ງ "ສາຂາ" ຈາກມັນແລະຂຽນຕົວເລກດຽວກັນໃສ່ທ້າຍຂອງມັນ. ຕົວເລກຫຼັກບໍ່ສາມາດຂະຫຍາຍເຂົ້າໄປໃນປັດໃຈທີ່ນ້ອຍກວ່າໄດ້, ສະນັ້ນພຽງແຕ່ຍ້າຍພວກມັນລົງໃນລະດັບໃດນຶ່ງ.
   • ຕົວຢ່າງ: 2 ເປັນຫຼັກ. ພຽງແຕ່ຍ້າຍ 2 ຈາກແຖວທີສອງໄປຫາແຖວທີສາມ:
   •      24
   •       /
   •    2   12
   •   /       /
   • 2     2   6
8. 8 ສືບຕໍ່ແຍກຕົວເລກອອກໄປຈົນກວ່າເຈົ້າຈະເຫຼືອພຽງແຕ່ຕົວເລກທໍາອິດ. ກວດເບິ່ງທຸກ line ເສັ້ນໃof່ຂອງຕົ້ນໄມ້. ຖ້າຢ່າງ ໜ້ອຍ ໜຶ່ງ ໃນປັດໃຈໃis່ບໍ່ແມ່ນຕົວເລກຫຼັກ, ປັດໄຈມັນແລະຂຽນແຖວໃ່. ໃນທີ່ສຸດ, ເຈົ້າຈະເຫຼືອພຽງແຕ່ຕົວເລກທີ່ເປັນຕົວເລກ.
   • ຕົວຢ່າງ: 6 ບໍ່ແມ່ນຕົວເລກ ສຳ ຄັນ, ສະນັ້ນມັນຄວນຈະຖືກຄິດໄລ່ດ້ວຍປັດໃຈຄືກັນ. ໃນເວລາດຽວກັນ, 2 ເປັນຕົວເລກທີ່ສໍາຄັນ, ແລະພວກເຮົາເອົາສອງອັນສອງອັນໄປສູ່ລະດັບຕໍ່ໄປ:
   •         24
   •          /
   •       2    12
   •      /       /
   •    2     2    6
   •   /      /      /
   • 2     2      2   3
9. 9 ຂຽນແຖວສຸດທ້າຍເປັນຜະລິດຕະພັນຂອງປັດໃຈຫຼັກ. ໃນທີ່ສຸດ, ເຈົ້າຈະເຫຼືອພຽງແຕ່ຕົວເລກທີ່ເປັນຕົວເລກ. ເມື່ອສິ່ງນີ້ເກີດຂຶ້ນ, ການສ້າງປັດໃຈຫຼັກແມ່ນ ສຳ ເລັດ. ແຖວສຸດທ້າຍແມ່ນຊຸດຂອງຕົວຢ່າງ, ຜະລິດຕະພັນທີ່ໃຫ້ຕົວເລກຕົ້ນສະບັບ.
   • ກວດເບິ່ງຄໍາຕອບຂອງເຈົ້າ: ຄູນເລກໃນແຖວສຸດທ້າຍ. ຜົນໄດ້ຮັບຄວນຈະເປັນຕົວເລກເດີມ.
   • ຕົວຢ່າງ: ແຖວສຸດທ້າຍຂອງຕົ້ນໄມ້ປັດໃຈປະກອບມີຕົວເລກ 2 ແລະ 3. ທັງສອງຕົວເລກເຫຼົ່ານີ້ເປັນຕົວເລກຫຼັກ, ສະນັ້ນການລະລາຍຈະສໍາເລັດສົມບູນ. ດັ່ງນັ້ນ, ປັດໄຈຫຼັກຂອງ 24 ມີຮູບແບບດັ່ງນີ້: 24 = 2 x 2 x 2 x 3.
   • ລຳ ດັບຂອງປັດໃຈບໍ່ ສຳ ຄັນ. ການຍ່ອຍສະຫຼາຍຍັງສາມາດຂຽນເປັນ 2 x 3 x 2 x 2.
10. 10 ເຮັດໃຫ້ ຄຳ ຕອບຂອງເຈົ້າງ່າຍຂຶ້ນໂດຍການໃຊ້ເຄື່ອງexpາຍເລກ ກຳ ລັງ, ຖ້າຕ້ອງການ. ຖ້າເຈົ້າຄຸ້ນເຄີຍກັບການຂະຫຍາຍຕົວເລກ, ເຈົ້າສາມາດຂຽນຄໍາຕອບໃສ່ໃນຮູບແບບທີ່ງ່າຍກວ່າ.ຈື່ໄວ້ວ່າຖານຖືກຂຽນຢູ່ທາງລຸ່ມ, ແລະຕົວເລກຕົວເລກຊີ້ບອກວ່າຄວນຄູນດ້ວຍຕົວມັນເອງຈັກເທື່ອ.
    • ຕົວຢ່າງ: ຕົວເລກ 2 ເກີດຂຶ້ນຈັກເທື່ອໃນການສະຫລາຍຕົວ 2 x 2 x 2 x 3? ສາມເທື່ອ, ດັ່ງນັ້ນ ສຳ ນວນ 2 x 2 x 2 ສາມາດຂຽນເປັນ 2. ໃນເຄື່ອງnotາຍງ່າຍified, ພວກເຮົາໄດ້ຮັບ 2 x 3.

ສ່ວນທີ 2 ຂອງ 2: ການ ນຳ ໃຊ້ປັດໃຈຫຼັກ

1. 1 ຊອກຕົວຫານທີ່ມີ ຈຳ ນວນຫຼາຍທີ່ສຸດຂອງຕົວເລກສອງຕົວ. ຕົວຫານສ່ວນໃຫຍ່ທີ່ສຸດ (GCD) ຂອງສອງຕົວເລກແມ່ນຕົວເລກສູງສຸດທີ່ຕົວເລກທັງສອງສາມາດຫານໄດ້ໂດຍບໍ່ມີຕົວເລກເຫຼືອ. ຕົວຢ່າງຂ້າງລຸ່ມນີ້ສະແດງໃຫ້ເຫັນວິທີການນໍາໃຊ້ປັດໃຈຕົ້ນຕໍເພື່ອຊອກຫາຕົວຫານສ່ວນໃຫຍ່ທີ່ສຸດຂອງ 30 ແລະ 36.
   • ໃຫ້ເອົາຕົວເລກທັງສອງມາເປັນປັດໃຈຫຼັກ. ສໍາລັບ 30, ການສ້າງປັດໃຈແມ່ນ 2 x 3 x 5. ຈໍານວນ 36 ແມ່ນໄດ້ເນົ່າເປື່ອຍລົງເປັນປັດໃຈຕົ້ນຕໍດັ່ງນີ້: 2 x 2 x 3 x 3.
   • ໃຫ້ຊອກຫາຕົວເລກທີ່ເກີດຂຶ້ນຢູ່ໃນການຂະຫຍາຍທັງສອງຢ່າງ. ໃຫ້ເອົາຕົວເລກນີ້ອອກໃນທັງສອງລາຍຊື່ແລະຂຽນມັນໃສ່ແຖວໃ່. ຕົວຢ່າງ, 2 ເກີດຂື້ນໃນສອງການຂະຫຍາຍ, ດັ່ງນັ້ນພວກເຮົາຂຽນ 2 ຢູ່ໃນເສັ້ນໃ່. ຫຼັງຈາກນັ້ນ, ພວກເຮົາມີ 30 = 2 x 3 x 5 ແລະ 36 = 2 x 2 x 3 x 3.
   • ເຮັດຊ້ ຳ ຂັ້ນຕອນນີ້ຈົນກວ່າຈະບໍ່ມີປັດໃຈທົ່ວໄປເຫຼືອຢູ່ໃນການຂະຫຍາຍ. ທັງສອງລາຍການຍັງລວມເອົາເລກ 3, ດັ່ງນັ້ນໃນແຖວໃyou່ເຈົ້າສາມາດຂຽນໄດ້ 2 ແລະ 3... ຈາກນັ້ນປຽບທຽບການຂະຫຍາຍອີກຄັ້ງ: 30 = 2 x 3 x 5 ແລະ 36 = 2 x 2 x 3 x 3. ດັ່ງທີ່ເຈົ້າເຫັນ, ບໍ່ມີປັດໃຈທົ່ວໄປທີ່ປະໄວ້ຢູ່ໃນພວກມັນ.
   • ເພື່ອຊອກຫາປັດໃຈ ທຳ ມະດາທີ່ໃຫຍ່ທີ່ສຸດ, ຊອກຫາຜົນຜະລິດຂອງປັດໃຈທົ່ວໄປທັງົດ. ໃນຕົວຢ່າງຂອງພວກເຮົາ, ເຫຼົ່ານີ້ແມ່ນ 2 ແລະ 3, ສະນັ້ນ gcd ແມ່ນ 2 x 3 = 6... ນີ້ແມ່ນຕົວເລກໃຫຍ່ສຸດທີ່ຫານຕົວເລກ 30 ແລະ 36 ເທົ່າກັນ.
2. 2 ດ້ວຍຄວາມຊ່ວຍເຫຼືອຂອງ GCD, ເຈົ້າສາມາດເຮັດໃຫ້ເສດສ່ວນງ່າຍຂຶ້ນ. ຖ້າເຈົ້າສົງໃສວ່າເສດສ່ວນ ໜຶ່ງ ສາມາດຖືກຍົກເລີກໄດ້, ໃຫ້ໃຊ້ປັດໃຈທົ່ວໄປທີ່ຍິ່ງໃຫຍ່ທີ່ສຸດ. ຊອກຫາ GCD ຂອງຕົວເສດແລະຕົວຫານໂດຍໃຊ້ຂັ້ນຕອນຂ້າງເທິງ. ຈາກນັ້ນຫານຕົວຫານແລະຕົວຫານຂອງເສດສ່ວນດ້ວຍຕົວເລກນັ້ນ. ຜົນກໍຄື, ເຈົ້າໄດ້ຮັບສ່ວນປະກອບອັນດຽວກັນໃນຮູບແບບທີ່ງ່າຍກວ່າ.
   • ຍົກຕົວຢ່າງ, ໃຫ້ເຮົາເຮັດໃຫ້ສ່ວນປະກອບງ່າຍຂຶ້ນ /₃₆... ດັ່ງທີ່ພວກເຮົາໄດ້ກ່າວມາຂ້າງເທິງ, ສໍາລັບ 30 ແລະ 36, GCD ແມ່ນ 6, ສະນັ້ນພວກເຮົາແບ່ງຕົວຫານແລະຕົວຫານດ້ວຍ 6:
   • 30 ÷ 6 = 5
   • 36 ÷ 6 = 6
   • /₃₆ = /₆
3. 3 ຊອກຫາຕົວຄູນທີ່ນ້ອຍທີ່ສຸດຂອງສອງຕົວເລກ. ຕົວຄູນທົ່ວໄປ ໜ້ອຍ ທີ່ສຸດ (LCM) ຂອງສອງຕົວເລກແມ່ນຕົວເລກນ້ອຍສຸດທີ່ສາມາດຫານໄດ້ທັງສອງ ຈຳ ນວນເທົ່າກັນ. ຕົວຢ່າງ, LCM ຂອງ 2 ແລະ 3 ແມ່ນ 6 ເພາະວ່າມັນເປັນຕົວເລກນ້ອຍສຸດທີ່ສາມາດຫານໄດ້ດ້ວຍ 2 ແລະ 3. ຂ້າງລຸ່ມນີ້ແມ່ນຕົວຢ່າງຂອງການຄົ້ນຫາ LCM ໂດຍໃຊ້ປັດໃຈຫຼັກ:
   • ເລີ່ມຕົ້ນດ້ວຍສອງປັດໃຈຫຼັກ. ສໍາລັບຕົວຢ່າງ, ສໍາລັບ 126, ຕົວປະກອບສາມາດຂຽນເປັນ 2 x 3 x 3 x 7. ຈໍານວນ 84 ສາມາດສະຫລາຍຕົວເປັນປັດໃຈຕົ້ນຕໍໄດ້ຄື 2 x 2 x 3 x 7.
   • ໃຫ້ສົມທຽບຈໍານວນເທື່ອທີ່ແຕ່ລະປັດໃຈເກີດຂຶ້ນຢູ່ໃນການຂະຫຍາຍຕົວ. ເລືອກລາຍການບ່ອນທີ່ຕົວຄູນເກີດຂຶ້ນ ຈຳ ນວນຄັ້ງສູງສຸດ, ແລະວົງມົນໃສ່ບ່ອນນີ້. ຕົວຢ່າງ, ຕົວເລກ 2 ປາກົດຄັ້ງດຽວໃນການຂະຫຍາຍຕົວສໍາລັບ 126 ແລະສອງຄັ້ງໃນລາຍການເປັນ 84, ດັ່ງນັ້ນເຈົ້າຄວນຈະເປັນວົງມົນ 2 x 2 ຢູ່ໃນລາຍການປັດໃຈທີສອງ.
   • ເຮັດຊ້ ຳ ຂັ້ນຕອນນີ້ ສຳ ລັບຕົວຄູນແຕ່ລະອັນ. ຕົວຢ່າງ, 3 ແມ່ນພົບເຫັນຫຼາຍໃນການຂະຫຍາຍ ທຳ ອິດ, ສະນັ້ນເຈົ້າຄວນຈະວົງມົນຢູ່ໃນນັ້ນ 3 x 3... ຕົວເລກ 7 ປະກົດຂຶ້ນເທື່ອດຽວຢູ່ໃນລາຍການທັງສອງ, ສະນັ້ນພວກເຮົາຈະໄປວົງມົນ 7 (ມັນບໍ່ສໍາຄັນຢູ່ໃນລາຍການອັນໃດ, ຖ້າປັດໄຈທີ່ເກີດຂຶ້ນຢູ່ໃນທັງສອງລາຍການມີຈໍານວນຄັ້ງດຽວກັນ).
   • ເພື່ອຊອກຫາ LCM, ໃຫ້ຄູນຕົວເລກທັງ.ົດທີ່ເປັນວົງມົນ. ໃນຕົວຢ່າງຂອງພວກເຮົາ, ຕົວຄູນທົ່ວໄປ ໜ້ອຍ ທີ່ສຸດຂອງ 126 ແລະ 84 ແມ່ນ 2 x 2 x 3 x 3 x 7 = 252... ນີ້ແມ່ນຕົວເລກທີ່ນ້ອຍທີ່ສຸດທີ່ສາມາດຫານໄດ້ດ້ວຍ 126 ແລະ 84 ໂດຍບໍ່ມີສ່ວນທີ່ເຫຼືອ.
4. 4 ໃຊ້ LCM ເພື່ອເພີ່ມເສດສ່ວນ. ເມື່ອເພີ່ມສອງເສດສ່ວນ, ມັນ ຈຳ ເປັນທີ່ຈະ ນຳ ພວກມັນມາຫານຕົວຫານທົ່ວໄປ. ເພື່ອເຮັດສິ່ງນີ້, ຊອກຫາ LCM ຂອງສອງຕົວຫານ. ຈາກນັ້ນ, ຄູນຕົວຫານແລະຕົວຫານຂອງແຕ່ລະເສດສ່ວນດ້ວຍຕົວເລກດັ່ງກ່າວທີ່ຕົວຫານຂອງເສດສ່ວນເທົ່າກັບ LCM. ຫຼັງຈາກນັ້ນ, ເຈົ້າສາມາດເພີ່ມເສດສ່ວນ.
   • ຕົວຢ່າງ, ເຈົ້າຕ້ອງການຊອກຫາ ຈຳ ນວນ /₆ + /₂₁.
   • ການນໍາໃຊ້ວິທີການຂ້າງເທິງ, ເຈົ້າສາມາດຊອກຫາ LCM ສໍາລັບ 6 ແລະ 21. ມັນແມ່ນ 42.
   • ພວກເຮົາປ່ຽນອັດຕາສ່ວນ₆ ເພື່ອໃຫ້ຕົວຫານຂອງມັນແມ່ນ 42. ເພື່ອເຮັດສິ່ງນີ້, ເຈົ້າຕ້ອງຫານ 42 ດ້ວຍ 6: 42 ÷ 6 = 7.₆ x /₇ = /₄₂.
   • ເພື່ອ ນຳ ເອົາເສດສ່ວນທີສອງມາໃຫ້ຕົວຫານ 42, ຫານ 42 ດ້ວຍ 21: 42 ÷ 21 = 2. ຄູນຕົວຫານແລະຕົວຫານຂອງເສດສ່ວນໂດຍ 2: /₂₁ x /₂ = /₄₂.
   • ຫຼັງຈາກເສດສ່ວນໄດ້ຖືກຫຼຸດລົງເປັນຕົວຫານດຽວກັນ, ພວກມັນສາມາດຖືກເພີ່ມເຂົ້າໄດ້ຢ່າງງ່າຍດາຍ: /₄₂ + /₄₂ = /₄₂.

ຕົວຢ່າງຂອງ ໜ້າ ວຽກ

• ພະຍາຍາມແກ້ໄຂບັນຫາຢູ່ລຸ່ມນີ້ດ້ວຍຕົວເຈົ້າເອງ.ຖ້າເຈົ້າຄິດວ່າເຈົ້າໄດ້ຮັບຄໍາຕອບທີ່ຖືກຕ້ອງ, ໃຫ້ເນັ້ນດ້ວຍເມົ້າວາງບ່ອນຫຼັງຈໍ້າສອງເມັດໃນຄໍາຖະແຫຼງບັນຫາ. ວຽກງານສຸດທ້າຍແມ່ນຫຍຸ້ງຍາກທີ່ສຸດ.
• ຊອກຫາປັດໃຈຫຼັກຂອງ 16: 2 x 2 x 2 x 2
• ຂຽນ ຄຳ ຕອບຂອງເຈົ້າໃສ່ໃນຮູບແບບເລກ ກຳ ລັງ: 2
• ຊອກຫາປັດໃຈຫຼັກຂອງ 45: 3 x 3 x 5
• ຂຽນ ຄຳ ຕອບຂອງເຈົ້າໃສ່ໃນຮູບແບບເລກ ກຳ ລັງ: 3 x 5
• ຊອກຫາປັດໃຈຫຼັກຂອງ 34: 2 x 17
• ຊອກຫາປັດໃຈຫຼັກຂອງ 154: 2 x 7 x 11
• ຊອກຫາປັດໃຈຕົ້ນຕໍ ສຳ ລັບ 8 ແລະ 40, ແລະຈາກນັ້ນ ກຳ ນົດປັດໃຈ ທຳ ມະດາທີ່ໃຫຍ່ທີ່ສຸດຂອງພວກເຂົາ: ປັດໄຈຫຼັກຂອງ 8 ແມ່ນ 2 x 2 x 2 x 2; ປັດໃຈຫຼັກຂອງ 40 ແມ່ນ 2 x 2 x 2 x 5; GCD ຂອງສອງຕົວເລກ 2 x 2 x 2 = 6.
• ຊອກຫາຕົວປະກອບຫຼັກ ສຳ ລັບ 18 ແລະ 52 ແລະຊອກຫາຕົວຄູນ ໜ້ອຍ ທີ່ສຸດຂອງພວກມັນ: ຕົວຄູນຫຼັກຂອງ 18 ແມ່ນ 2 x 3 x 3; ປັດໃຈຫຼັກຂອງ 52 ແມ່ນ 2 x 2 x 13; LCM ຂອງສອງຕົວເລກແມ່ນ 2 x 2 x 3 x 3 x 13 = 468.

ຄໍາແນະນໍາ

• ຕົວເລກແຕ່ລະຄົນມີລັກສະນະການປັດໄຈທີ່ເປັນເອກະລັກຂອງມັນ. ມັນບໍ່ ສຳ ຄັນວ່າເຈົ້າຈະພົບເຫັນການຂະຫຍາຍອັນນີ້ໄດ້ແນວໃດ, ເຈົ້າຄວນຈົບລົງດ້ວຍ ຄຳ ຕອບດຽວກັນ. ອັນນີ້ເອີ້ນວ່າທິດສະດີພື້ນຖານຂອງເລກຄະນິດ.
• ແທນທີ່ຈະຂຽນຕົວເລກທີ່ ສຳ ຄັນຄືນໃon່ຢູ່ໃນແຖວໃof່ຂອງຕົ້ນໄມ້ປັດໃຈແຕ່ລະຄັ້ງ, ເຈົ້າສາມາດປ່ອຍໃຫ້ມັນຢູ່ໃນສະຖານທີ່ແລະcircleາຍວົງມົນໃສ່ພວກມັນໄດ້. ໃນຕອນທ້າຍຂອງການຂະຫຍາຍຕົວ, ມັນຈະລວມເອົາທຸກປັດໃຈທີ່ມີວົງມົນ.
• ກວດເບິ່ງ ຄຳ ຕອບທີ່ເຈົ້າໄດ້ຮັບຢູ່ສະເີ. ເຈົ້າສາມາດເຮັດຜິດພາດແລະບໍ່ສັງເກດເຫັນມັນ.
• ກຽມພ້ອມສໍາລັບພາລະກິດທີ່ຫຼອກລວງ. ຖ້າເຈົ້າຖືກຖາມໃຫ້ຊອກຫາປັດໃຈຫຼັກຂອງຕົວເລກຫຼັກ, ບໍ່ ຈຳ ເປັນຕ້ອງເຮັດການ ຄຳ ນວນໃດ. ຕົວຢ່າງ, ສໍາລັບຈໍານວນ 17, ປັດໃຈຕົ້ນຕໍແມ່ນ 17; ຕົວເລກນີ້ບໍ່ສາມາດແຍກສະຫລາຍໄປເປັນປັດໃຈຫຼັກອື່ນ other ໄດ້.
• ປັດໃຈທົ່ວໄປທີ່ຍິ່ງໃຫຍ່ທີ່ສຸດແລະຕົວຄູນທົ່ວໄປ ໜ້ອຍ ທີ່ສຸດສາມາດພົບໄດ້ດ້ວຍຕົວເລກສາມຕົວຫຼືຫຼາຍກວ່ານັ້ນ.

ຄຳ ເຕືອນ

• ຕົ້ນໄມ້ຄູນອະນຸຍາດໃຫ້ເຈົ້າ ກຳ ນົດພຽງແຕ່ປັດໃຈຫຼັກ, ບໍ່ແມ່ນປັດໃຈທີ່ເປັນໄປໄດ້ທັງົດ.