ເນື້ອຫາ

• ເພື່ອກ້າວ
• ພາກທີ 1 ຂອງ 5: ຮຽນຮູ້ກົດລະບຽບພື້ນຖານຂອງພຶດຊະຄະນິດ
• ສ່ວນທີ 2 ຂອງ 5: ເຂົ້າໃຈຕົວແປ
• ພາກທີ 3 ຂອງ 5: ແກ້ສົມຜົນໂດຍການ ກຳ ຈັດ
• ສ່ວນທີ 4 ຂອງ 5: ເລັ່ງຄວາມສາມາດດ້ານຄະນິດສາດຂອງທ່ານ
• ພາກທີ 5 ຂອງ 5: ການ ສຳ ຫຼວດຫົວຂໍ້ທີ່ກ້າວ ໜ້າ
• ຄຳ ແນະ ນຳ

ການຮຽນກ່ຽວກັບພຶດຊະຄະນິດແມ່ນມີຄວາມ ສຳ ຄັນທີ່ຈະສາມາດພັດທະນາກັບເກືອບທຸກພາກສ່ວນຂອງຄະນິດສາດໃນຊັ້ນມັດທະຍົມແລະຊັ້ນສູງ. ທຸກໆລະດັບຂອງຄະນິດສາດຖືກສ້າງຂື້ນບົນພື້ນຖານ, ແລະດ້ວຍນັ້ນ, ທຸກລະດັບຄະນິດສາດແມ່ນມີຄວາມ ສຳ ຄັນເປັນພິເສດ. ເຖິງຢ່າງໃດກໍ່ຕາມ, ເຖິງແມ່ນວ່າທັກສະພື້ນຖານທີ່ສຸດສາມາດເປັນເລື່ອງຍາກ ສຳ ລັບຜູ້ເລີ່ມທີ່ຈະເຂົ້າໃຈໃນເວລາທີ່ປະເຊີນ ​​ໜ້າ ກັບພວກເຂົາເປັນເທື່ອ ທຳ ອິດ. ຖ້າທ່ານ ກຳ ລັງດີ້ນລົນກັບຫົວຂໍ້ຄະນິດສາດພື້ນຖານ, ຢ່າກັງວົນ. ດ້ວຍ ຄຳ ອະທິບາຍເລັກໆນ້ອຍໆ, ມີຕົວຢ່າງງ່າຍໆແລະ ຄຳ ແນະ ນຳ ບາງຢ່າງເພື່ອປັບປຸງທັກສະຂອງທ່ານ, ທ່ານຈະເປັນປະລິນຍາໂທຄະນິດສາດໃນໄວໆນີ້.

ເພື່ອກ້າວ

ພາກທີ 1 ຂອງ 5: ຮຽນຮູ້ກົດລະບຽບພື້ນຖານຂອງພຶດຊະຄະນິດ

1. ທົບທວນທັກສະພື້ນຖານຂອງຄະນິດສາດ. ເພື່ອຮຽນຮູ້ພຶດຊະຄະນິດທ່ານຈະຕ້ອງຮູ້ທັກສະພື້ນຖານເຊັ່ນ: ການເພີ່ມ, ການຫັກລົບ, ການຄູນແລະການແບ່ງ. ທັກສະດ້ານຄະນິດສາດເຫຼົ່ານີ້ເມື່ອທ່ານຮຽນພວກເຂົາໃນຊັ້ນປະຖົມແມ່ນມີຄວາມ ຈຳ ເປັນກ່ອນທີ່ທ່ານຈະເລີ່ມຮຽນກ່ຽວກັບພຶດຊະຄະນິດ. ຖ້າທ່ານບໍ່ໄດ້ຮຽນຮູ້ທັກສະເຫຼົ່ານີ້, ມັນຈະເປັນການຍາກທີ່ຈະຮຽນຮູ້ແນວຄວາມຄິດທີ່ສັບສົນກວ່າທີ່ຖືກປົກຄຸມດ້ວຍຄະນິດສາດ. ຖ້າທ່ານຕ້ອງການເພີ່ມເຕີມກ່ຽວກັບການປະຕິບັດງານເຫຼົ່ານີ້, ໃຫ້ກວດເບິ່ງ wikiHow ສຳ ລັບບົດຂຽນກ່ຽວກັບພື້ນຖານຂອງເລກຄະນິດສາດ.
   • ບໍ່ ຈຳ ເປັນຕ້ອງເກັ່ງດ້ານຄະນິດສາດທາງຈິດເພື່ອຈະສາມາດເຮັດຄະນິດສາດໄດ້ດີ. ປົກກະຕິແລ້ວທ່ານຈະໄດ້ຮັບອະນຸຍາດໃຫ້ເຮັດວຽກກັບເຄື່ອງຄິດໄລ່ໃນໄລຍະຮຽນຄະນິດສາດເພື່ອປະຫຍັດເວລາໃນການປະເມີນແບບງ່າຍໆ. ໃນກໍລະນີໃດກໍ່ຕາມ, ທ່ານຄວນຈະສາມາດເຮັດເລກຄະນິດສາດໂດຍບໍ່ມີເຄື່ອງຄິດໄລ່, ໃນກໍລະນີທີ່ທ່ານບໍ່ໄດ້ຮັບອະນຸຍາດໃຫ້ໃຊ້ມັນ.
2. ຮຽນຮູ້ຄໍາສັ່ງຂອງການດໍາເນີນງານ. ສິ່ງ ໜຶ່ງ ທີ່ຍາກທີ່ສຸດໃນການແກ້ໄຂສົມຜົນຄະນິດສາດແມ່ນການຮູ້ບ່ອນທີ່ຈະເລີ່ມຕົ້ນ. ໂຊກດີ, ມີ ຄຳ ສັ່ງສະເພາະໃດ ໜຶ່ງ ທີ່ທ່ານສາມາດແກ້ໄຂບັນຫາເຫຼົ່ານີ້: ທຳ ອິດແມ່ນ ຄຳ ສັບໃນວົງເລັບ, ຫຼັງຈາກນັ້ນ ຄຳ ນຳ / ອຳ ນາດ, ຈາກນັ້ນຄູນ, ແບ່ງ, ເພີ່ມແລະສຸດທ້າຍການຫັກລົບ. mnemonic ທີ່ມີປະໂຫຍດ ສຳ ລັບການຈື່ ຈຳ ລຳ ດັບຂອງການປະຕິບັດງານແມ່ນ "ວິທີການ ກຳ ຈັດຄວາມລົ້ມເຫຼວ" (ຫຼືເປັນ ຄຳ ວ່າ HMWVDOA). ເບິ່ງ wikiHow ສຳ ລັບບົດຂຽນກ່ຽວກັບການ ນຳ ໃຊ້ ຄຳ ສັ່ງການ ດຳ ເນີນງານ. ເພື່ອເປັນການເຕືອນ, ນີ້ແມ່ນ ລຳ ດັບ ລຳ ດັບການ ດຳ ເນີນງານອີກຄັ້ງ ໜຶ່ງ:
   • ຮ.ຖັງນໍ້າມ
   • ມ.ຍົກສູງບົດບາດແປດ
   • W.ການດຶງຮາກ
   • V.ຄູນ
   • ງ.ສິບເອັດ
   • ອການນັບ
   • ກດຶງ
   • ຄໍາສັ່ງຂອງການດໍາເນີນງານແມ່ນສໍາຄັນໃນຄະນິດສາດ, ເພາະວ່າຄໍາສັ່ງທີ່ບໍ່ຖືກຕ້ອງສາມາດເຮັດໃຫ້ມີຄໍາຕອບທີ່ແຕກຕ່າງກັນ. ຕົວຢ່າງ: ຖ້າທ່ານມີປັນຫາ 8 + 2 × 5, ແລະທ່ານ ທຳ ອິດເພີ່ມ 2 ຫາ 8, ທ່ານຈະໄດ້ຮັບ 10 × 5 =50 ໃນການຕອບໂຕ້. ແຕ່ຖ້າທ່ານຄູນ 2 ໂດຍ 5 ກ່ອນ, ຫຼັງຈາກນັ້ນມັນກໍ່ຕາມທີ່ 8 + 10 =18. ພຽງແຕ່ ຄຳ ຕອບທີສອງແມ່ນຖືກຕ້ອງ.
3. ຮຽນຮູ້ການໃຊ້ເລກລົບ. ມັນເປັນເລື່ອງ ທຳ ມະດາທີ່ຈະໃຊ້ເລກລົບໃນຄະນິດສາດ, ສະນັ້ນມັນເປັນຄວາມຄິດທີ່ດີທີ່ຈະທົບທວນວິທີການເພີ່ມ, ຫັກລົບ, ທະວີຄູນແລະແບ່ງປັນຕົວເລກລົບກ່ອນທີ່ຈະກ້າວໄປສູ່ພຶດຊະຄະນິດ. ຂ້າງລຸ່ມນີ້ແມ່ນພຽງບາງສ່ວນພື້ນຖານຂອງການເຮັດວຽກກັບເລກລົບທີ່ທ່ານ ຈຳ ເປັນຕ້ອງຈື່ - ສຳ ລັບຂໍ້ມູນເພີ່ມເຕີມ, ເບິ່ງບົດຄວາມຂອງ wikiHow ກ່ຽວກັບການເພີ່ມ, ການຫັກລົບ, ການແບ່ງສ່ວນແລະການຄູນເລກລົບ.
   • ຢູ່ໃນເສັ້ນ ໝາຍ ເລກ, ຮຸ່ນລົບຂອງຕົວເລກແມ່ນຢູ່ໄກຈາກສູນເທົ່າກັບທາງບວກ, ແຕ່ໃນທິດທາງກົງກັນຂ້າມ.
   • ການເພີ່ມສອງຕົວເລກລົບເຮັດໃຫ້ຜົນລວມ ກະທົບທາງລົບຫຼາຍ (ເວົ້າອີກຢ່າງ ໜຶ່ງ, ຕົວເລກແມ່ນນັບມື້ນັບໃຫຍ່ຂື້ນ, ແຕ່ຍ້ອນວ່າຕົວເລກບໍ່ດີມັນແມ່ນຕົວເລກທີ່ຕ່ ຳ ກວ່າ)
   • ສອງສັນຍານລົບຈະຍົກເລີກເຊິ່ງກັນແລະກັນອອກ - ການຫັກລົບເລກລົບແມ່ນຄືກັນກັບການເພີ່ມເລກບວກ.
   • ການຄູນຫລືແບ່ງປັນສອງຕົວເລກລົບໃຫ້ ຄຳ ຕອບທີ່ເປັນບວກ.
   • ການຄູນຫລືແບ່ງປັນຕົວເລກໃນແງ່ບວກແລະເລກລົບກໍ່ໃຫ້ ຄຳ ຕອບທີ່ບໍ່ດີ.
4. ຮຽນຮູ້ວິທີການຈັດແຈງບັນຫາທີ່ຍາວນານ. ໃນຂະນະທີ່ບັນຫາກ່ຽວກັບພຶດຊະຄະນິດງ່າຍໆມັກຈະແກ້ໄຂໄດ້, ບັນຫາທີ່ສັບສົນຫຼາຍສາມາດໃຊ້ຫຼາຍຂັ້ນຕອນເພື່ອເຮັດໃຫ້ ສຳ ເລັດ. ເພື່ອຫລີກລ້ຽງຄວາມຜິດພາດ, ຢ່າງ ໜ້ອຍ ກໍ່ຄວນເລີ່ມຕົ້ນສາຍ ໃໝ່ ທຸກໆຄັ້ງ, ທັນທີທີ່ທ່ານກ້າວຕໍ່ໄປອີກບາດກ້າວ ໜຶ່ງ ໃນການແກ້ໄຂບັນຫາ. ຖ້າທ່ານ ກຳ ລັງປະຕິບັດກັບການປຽບທຽບກັບ ຄຳ ສັບໃນສອງດ້ານຂອງເຄື່ອງ ໝາຍ ທີ່ເທົ່າກັນ, ພະຍາຍາມຂຽນຕົວອັກສອນເຫຼົ່ານີ້ ("=") ໜຶ່ງ ດ້ານລຸ່ມ. ໂດຍວິທີນັ້ນ, ຂໍ້ຜິດພາດໃດໆໃນການຄິດໄລ່ຂອງທ່ານຈະງ່າຍຂື້ນກວ່າເກົ່າ.
   • ຕົວຢ່າງ, ເພື່ອແກ້ສົມຜົນ 9/3 - 5 + 3 × 4, ພວກເຮົາສັ່ງບັນຫາຂອງພວກເຮົາຄືດັ່ງນີ້:

     9/3 - 5 + 3 × 4

     9/3 - 5 + 12

     3 - 5 + 12

     3 + 7

     10

ສ່ວນທີ 2 ຂອງ 5: ເຂົ້າໃຈຕົວແປ

1. ຊອກຫາສັນຍາລັກທີ່ບໍ່ແມ່ນຕົວເລກ. ໃນຄະນິດສາດ, ທ່ານຈັດການກັບຕົວອັກສອນແລະສັນຍາລັກໃນບັນຫາເລກຂອງທ່ານ, ແທນທີ່ຈະເປັນພຽງຕົວເລກ. ເຫຼົ່ານີ້ເອີ້ນວ່າຕົວແປ. ຕົວແປບໍ່ມີຄວາມຫຍຸ້ງຍາກຍ້ອນວ່າພວກເຂົາເບິ່ງຄືວ່າ - ພວກເຂົາແມ່ນວິທີການທີ່ຈະເປັນຕົວແທນຂອງຕົວເລກທີ່ມີຄ່າທີ່ບໍ່ຮູ້ຈັກ. ຂ້າງລຸ່ມນີ້ແມ່ນບາງຕົວຢ່າງທົ່ວໄປຂອງຕົວແປໃນພຶດຊະຄະນິດ:
   • ຕົວອັກສອນເຊັ່ນ x, y, z, a, b, ແລະ c
   • ຕົວອັກສອນກະເຣັກເຊັ່ນ: theta, ຫຼືθ
   • ຢ່າສັງເກດວ່າ ທັງ ໝົດ ສັນຍາລັກແມ່ນຕົວແປທີ່ບໍ່ຮູ້ຈັກ. ຍົກຕົວຢ່າງ, pi ຫຼືπ, ສະເຫມີເທົ່າກັນ (ກົມ) 3.1459.
2. ຄິດວ່າຕົວແປເປັນຕົວເລກ "ບໍ່ຮູ້". ດັ່ງທີ່ໄດ້ລະບຸໄວ້ຂ້າງເທິງ, ຕົວປ່ຽນແປງໂດຍທົ່ວໄປແມ່ນພຽງແຕ່ຕົວເລກທີ່ມີຄ່າທີ່ບໍ່ຮູ້. ໃນຄໍາສັບຕ່າງໆອື່ນໆ, ມີ ຈໍານວນຫນຶ່ງ ເຊິ່ງສາມາດເອົາຕົວແທນຂອງຕົວແປເພື່ອເຮັດໃຫ້ສົມຜົນເຮັດວຽກ. ໂດຍປົກກະຕິແລ້ວ, ຈຸດປະສົງຂອງບັນຫາກ່ຽວກັບພຶດຊະຄະນິດແມ່ນເພື່ອຄິດອອກວ່າຕົວແປນັ້ນແມ່ນຫຍັງ - ຄິດວ່າມັນແມ່ນ "ເລກທີ່ລຶກລັບ" ທີ່ທ່ານ ກຳ ລັງພະຍາຍາມຄົ້ນພົບ.
   • ຕົວຢ່າງ, ໃນສົມຜົນ 2x + 3 = 11, x ແມ່ນຕົວແປ. ນີ້ ໝາຍ ຄວາມວ່າມີຄ່າທີ່ແນ່ນອນທີ່ສາມາດທົດແທນ x, ເຮັດໃຫ້ເບື້ອງຊ້າຍຂອງສະມະການເທົ່າກັບ 11. ເນື່ອງຈາກວ່າ 2 × 4 + 3 = 11, ໃນກໍລະນີນີ້, x =4.
   • ວິທີທີ່ງ່າຍທີ່ຈະເຂົ້າໃຈຕົວແປແມ່ນການທົດແທນພວກມັນດ້ວຍເຄື່ອງ ໝາຍ ຄຳ ຖາມໃນບັນຫາກ່ຽວກັບພຶດຊະຄະນິດ. ຍົກຕົວຢ່າງ, ຂຽນ ໃໝ່ ສົມຜົນ 2 + 3 + x = 9 ເປັນ 2 + 3 + ?=.. ນີ້ແມ່ນວິທີງ່າຍໆທີ່ຈະເຫັນຈຸດປະສົງແມ່ນຫຍັງ - ພວກເຮົາ ຈຳ ເປັນຕ້ອງຄິດໄລ່ ຈຳ ນວນໃດທີ່ຈະເພີ່ມໃສ່ 2 + 3 = 5 ເພື່ອໃຫ້ໄດ້ 9 ເປັນ ຄຳ ຕອບ. ຄຳ ຕອບແມ່ນອີກເທື່ອ ໜຶ່ງ 4, ແນ່​ນອນ.
3. ຖ້າຕົວແປໃດ ໜຶ່ງ ປະກົດຂື້ນຫຼາຍຄັ້ງ, ໃຫ້ປ່ຽນແປງຕົວແປຕ່າງໆ. ເຈົ້າຈະເຮັດແນວໃດຖ້າຕົວແປດຽວກັນນີ້ປາກົດຫຼາຍຄັ້ງໃນສົມຜົນ? ໃນຂະນະທີ່ສິ່ງນີ້ອາດເບິ່ງຄືວ່າສະຖານະການທີ່ຫຼອກລວງ, ທ່ານສາມາດປະຕິບັດຕົວແປທີ່ທ່ານປະຕິບັດກັບຕົວເລກປົກກະຕິ - ເວົ້າອີກຢ່າງ ໜຶ່ງ, ທ່ານສາມາດເພີ່ມ, ຫັກອອກ, ແລະອື່ນໆຕາບໃດທີ່ທ່ານພຽງແຕ່ສົມທົບຕົວແປທີ່ເທົ່າກັນ. ເວົ້າອີກຢ່າງ ໜຶ່ງ, x + x = 2 ເທົ່າ, ແຕ່ x + y ບໍ່ເທົ່າກັບ 2xy.
   • ຍົກຕົວຢ່າງ, ເບິ່ງສົມຜົນ 2x + 1x = 9. ໃນກໍລະນີນີ້, ພວກເຮົາເພີ່ມ 2x ແລະ 1x ຮ່ວມກັນ, ດັ່ງນັ້ນພວກເຮົາໄດ້ຮັບ 3x = 9. ຕັ້ງແຕ່ 3 x 3 = 9, ດຽວນີ້ພວກເຮົາຮູ້ແລ້ວວ່າ x =3.
   • ໃຫ້ສັງເກດອີກເທື່ອ ໜຶ່ງ ວ່າທ່ານພຽງແຕ່ສາມາດເພີ່ມຕົວແປທີ່ເທົ່າກັບກັນແລະກັນ. ໃນສົມຜົນ 2x + 1y = 9, ພວກເຮົາບໍ່ສາມາດສົມທົບ 2x ແລະ 1y, ເພາະວ່ານີ້ແມ່ນສອງຕົວແປທີ່ແຕກຕ່າງກັນ.
   • ນີ້ກໍ່ແມ່ນຄວາມຖືກຕ້ອງໃນເວລາທີ່ຕົວແປ ໜຶ່ງ ມີຄວາມແຕກຕ່າງຈາກຕົວເລກອື່ນ. ຕົວຢ່າງ: ໃນສົມຜົນ 2x + 3x = 10, 2x ແລະ 3x ບໍ່ສາມາດລວມເຂົ້າກັນໄດ້, ເພາະວ່າຕົວແປ x ມີຕົວເລກທີ່ແຕກຕ່າງກັນ. ສຳ ລັບຂໍ້ມູນເພີ່ມເຕີມກ່ຽວກັບການເພີ່ມອະທິບາຍ, ເບິ່ງ wikiHow.

ພາກທີ 3 ຂອງ 5: ແກ້ສົມຜົນໂດຍການ ກຳ ຈັດ

1. ແຍກຕົວປ່ຽນໃນສົມຜົນ. ການແກ້ໄຂສົມຜົນໃນຄະນິດສາດໂດຍທົ່ວໄປກ່ຽວຂ້ອງກັບການພະຍາຍາມ ກຳ ນົດວ່າຕົວປ່ຽນແມ່ນຫຍັງ. ສົມຜົນ Algebraic ມັກຈະມີຕົວເລກແລະ / ຫຼືຕົວແປຢູ່ທັງສອງຂ້າງ, ເຊັ່ນນີ້: x + 2 = 9 × 4. ເພື່ອ ກຳ ນົດວ່າຕົວແປແມ່ນຫຍັງ, ທ່ານຈະຕ້ອງວາງມັນໄວ້ຢູ່ຂ້າງ ໜຶ່ງ ຂອງເຄື່ອງ ໝາຍ ເທົ່າກັນ. ສິ່ງທີ່ຍັງເຫລືອຢູ່ອີກເບື້ອງ ໜຶ່ງ ຂອງເຄື່ອງ ໝາຍ ເທົ່າກັນແມ່ນ ຄຳ ຕອບ.
   • ໃນຕົວຢ່າງ (x + 2 = 9 × 4), ເພື່ອແຍກ x ຢູ່ເບື້ອງຊ້າຍຂອງສົມຜົນ, ພວກເຮົາຕ້ອງ ກຳ ຈັດ "+ 2". ເພື່ອເຮັດສິ່ງນີ້, ພວກເຮົາຫັກ 2 ຈາກຂ້າງນີ້, ເຮັດໃຫ້ພວກເຮົາ x = 9 × 4. ເພື່ອເຮັດໃຫ້ທັງສອງດ້ານຂອງສົມຜົນເທົ່າທຽມກັນ, ພວກເຮົາຍັງຕ້ອງຫັກ 2 ຈາກອີກຂ້າງ ໜຶ່ງ. ສິ່ງນີ້ເຮັດໃຫ້ພວກເຮົາ x = 9 × 4 - 2. ອີງຕາມຄໍາສັ່ງຂອງການປະຕິບັດງານ, ພວກເຮົາຄູນກ່ອນ, ຫຼັງຈາກນັ້ນຫັກອອກ, ແລະພວກເຮົາໄດ້ຮັບຄໍາຕອບ x = 36 - 2 =34.
2. ລົບລ້າງການເພີ່ມເຕີມໂດຍການຫັກລົບ (ແລະໃນທາງກັບກັນ). ດັ່ງທີ່ພວກເຮົາໄດ້ເຫັນຂ້າງເທິງ, ການແຍກ x ຢູ່ຂ້າງ ໜຶ່ງ ຂອງເຄື່ອງ ໝາຍ ເທົ່າກັນໂດຍປົກກະຕິແລ້ວແມ່ນກ່ຽວຂ້ອງກັບການພະຍາຍາມ ກຳ ຈັດຕົວເລກຢູ່ຂ້າງມັນ. ທ່ານເຮັດສິ່ງນີ້ໂດຍປະຕິບັດງານ "ກົງກັນຂ້າມ" ໃນທັງສອງດ້ານຂອງສົມຜົນ. ຍົກຕົວຢ່າງ, ໃນສົມຜົນ x + 3 = 0, ພວກເຮົາເອົາ "- 3" ຢູ່ທັງສອງດ້ານ, ເພາະວ່າມີ "+ 3" ຢູ່ຂ້າງ x. ນີ້ຈະແຍກ x ແລະໄດ້ຮັບ "-3" ອີກດ້ານ ໜຶ່ງ ຂອງເຄື່ອງ ໝາຍ ສະ ເໝີ ພາບ, ເຊັ່ນນີ້: x = -3.
   • ໂດຍທົ່ວໄປ, ການເພີ່ມແລະການຫັກລົບແມ່ນ "ກົງກັນຂ້າມ" - ວິທີການ ໜຶ່ງ ເຮັດວຽກ. ເບິ່ງຂ້າງລຸ່ມນີ້:

     ເມື່ອເພີ່ມ, ຫັກອອກ. ຕົວຢ່າງ: x + 9 = 3 → x = 3 - 9

     ເມື່ອຫັກລົບ, ເພີ່ມ. ຕົວຢ່າງ: x - 4 = 20 → x = 20 + 4

3. ລົບລ້າງການຄູນໂດຍແບ່ງ (ແລະກົງກັນຂ້າມ). ການຄູນແລະການແບ່ງຂັ້ນຕ່າງໆແມ່ນມີຄວາມຫຍຸ້ງຍາກຫຼາຍກວ່າທີ່ຈະເຮັດວຽກຮ່ວມກັບນອກ ເໜືອ ຈາກການເພີ່ມແລະການຫັກລົບ, ແຕ່ພວກເຂົາແບ່ງປັນຄວາມ ສຳ ພັນ "ກົງກັນຂ້າມ" ດຽວກັນ. ຖ້າທ່ານເຫັນ "× 3" ຢູ່ຂ້າງ ໜຶ່ງ, ທ່ານສາມາດ ກຳ ຈັດມັນໄດ້ໂດຍການແບ່ງທັງສອງດ້ານດ້ວຍ 3.
   • ດ້ວຍການຄູນແລະການແບ່ງ, ທ່ານຕ້ອງເຮັດການ ດຳ ເນີນງານທີ່ກົງກັນຂ້າມ ທຸກສິ່ງທຸກຢ່າງ ໃນອີກດ້ານ ໜຶ່ງ ຂອງເຄື່ອງ ໝາຍ ສະ ເໝີ ພາບ, ເຖິງແມ່ນວ່າມັນຈະມີຫລາຍກວ່າ ໜຶ່ງ ຕົວເລກ. ເບິ່ງຂ້າງລຸ່ມນີ້:

     ເມື່ອຄູນ, ແບ່ງອອກ. ຕົວຢ່າງ: 6x = 14 + 2 → x = (14 + 2)/6

     ເມື່ອແບ່ງປັນ, ຄູນ. ຕົວຢ່າງ: x / 5 = 25 → x = 25 × 5

4. ກຳ ຈັດອະໄວຍະວະໂດຍການເອົາຮາກຮຽບຮ້ອຍ (ແລະໃນທາງກັບກັນ). ຕົວແປແມ່ນຫົວຂໍ້ທີ່ກ້າວ ໜ້າ ໃນຄະນິດສາດ - ຖ້າທ່ານບໍ່ຮູ້ວ່າຈະເຮັດແນວໃດກັບມັນ, ໃຫ້ອ່ານບົດຄວາມຂອງ wikiHow ຂອງຜູ້ເລີ່ມຕົ້ນກ່ຽວກັບ ຄຳ ນຳ ສະ ເໜີ. ຕົວແປ "ກົງກັນຂ້າມ" ຂອງອະທິປະໄຕແມ່ນຮາກຖານຂອງຕົວເລກນັ້ນ. ຍົກຕົວຢ່າງ, ກົງກັນຂ້າມຂອງເລກ ກຳ ລັງເປັນຮາກສີ່ຫລ່ຽມ (√), ກົງກັນຂ້າມຂອງເລກ ກຳ ລັງແມ່ນຮາກ cube (√), ແລະອື່ນໆ.
   • ນີ້ສາມາດສັບສົນເລັກນ້ອຍ, ແຕ່ໃນກໍລະນີເຫຼົ່ານີ້ທ່ານຖືເອົາພື້ນທີ່ສີ່ຫລ່ຽມຂອງທັງສອງດ້ານເມື່ອກ່ຽວຂ້ອງກັບໂຕເລກ. ໃນທາງກົງກັນຂ້າມ, ທ່ານຍັງໃຊ້ ຄຳ ເວົ້າທີ່ສົມເຫດສົມຜົນຂອງທັງສອງດ້ານໃນເວລາຈັດການກັບຮາກສີ່ຫລ່ຽມ. ເບິ່ງຂ້າງລຸ່ມນີ້:

     ສຳ ລັບເລກ ກຳ ລັງ, ເອົາຮາກຮຽບຮ້ອຍ. ຕົວຢ່າງ: x = 49 → x =√49

     ສຳ ລັບຮາກ, ໃຊ້ເວລາອອກ. ຕົວຢ່າງ: √x = 12 → x =12

ສ່ວນທີ 4 ຂອງ 5: ເລັ່ງຄວາມສາມາດດ້ານຄະນິດສາດຂອງທ່ານ

1. ໃຊ້ຮູບເພື່ອເຮັດໃຫ້ການອອກ ກຳ ລັງກາຍແຈ່ມແຈ້ງຂື້ນ. ຖ້າທ່ານບໍ່ສາມາດສະ ເໜີ ບັນຫາກ່ຽວກັບພຶດຊະຄະນິດ, ໃຫ້ໃຊ້ເສັ້ນສະແດງຫຼືຮູບພາບເພື່ອສະແດງໃຫ້ເຫັນສົມຜົນ. ທ່ານຍັງສາມາດໃຊ້ກຸ່ມວັດຖຸ (ເຊັ່ນ: ທ່ອນໄມ້ຫລືຫຼຽນເງິນ) ຖ້າທ່ານມີມັນຢູ່ໃນມື.
   • ຍົກຕົວຢ່າງ, ພວກເຮົາແກ້ໄຂສົມຜົນ x + 2 = 3 ໂດຍໃຊ້ກ່ອງ (☐)

     x + 2 = 3

     ☒+☐☐=☐☐☐

     ໃນຈຸດນີ້, ໃຫ້ຫັກ 2 ຈາກທັງສອງດ້ານໂດຍການເອົາ 2 ກ່ອງ (☐☐) ທັງສອງດ້ານ:

     ☒+☐☐-☐☐=☐☐☐-☐☐

     ☒ = ☐, ຫຼື x =1

   • ຕົວຢ່າງອີກອັນ ໜຶ່ງ: 2 ເທົ່າ = 4

     ☒☒=☐☐☐☐

     ໃນຈຸດນີ້, ພວກເຮົາແບ່ງທັງສອງດ້ານເປັນສອງ, ແບ່ງກ່ອງໃສ່ແຕ່ລະດ້ານເປັນສອງກຸ່ມ:

     ☒|☒=☐☐|☐☐

     ☒ = ☐☐, ຫຼື x =2

2. ໃຊ້ "ການກວດສອບຕາມເຫດຜົນ" (ໂດຍສະເພາະເມື່ອເວົ້າເຖິງບັນຫາຕ່າງໆ). ເມື່ອທ່ານຕ້ອງການປ່ຽນບັນຫາໄປຫາສົມຜົນພຶດຊະຄະນິດ, ໃຫ້ກວດເບິ່ງສູດຂອງທ່ານໂດຍການລວມເອົາຄຸນຄ່າງ່າຍໆເຂົ້າໃນຕົວແປຕ່າງໆ. ສົມຜົນຂອງເຈົ້າແມ່ນຖືກຕ້ອງບໍເມື່ອ x = 0? ເມື່ອ x = 1? ເມື່ອ x = -1? ມັນງ່າຍທີ່ຈະເຮັດຜິດເລັກໆນ້ອຍໆໃນຂະນະທີ່ສັງເກດບາງສິ່ງບາງຢ່າງເຊັ່ນ: p = 6d ເມື່ອທ່ານ ໝາຍ ຄວາມວ່າ p = d / 6, ແຕ່ທ່ານຈະພົບກັບພວກມັນໄວໆນີ້ຖ້າທ່ານກວດເບິ່ງວຽກທີ່ທ່ານໄດ້ເຮັດກ່ອນທີ່ຈະກ້າວຕໍ່ໄປ.
   • ຕົວຢ່າງ: ສົມມຸດວ່າພວກເຮົາມີສະ ໜາມ ເຕະບານທີ່ຍາວກວ່າ 30 ແມັດກ່ວາມັນກວ້າງ. ພວກເຮົາໃຊ້ສົມຜົນ l = w + 30 ເພື່ອເປັນຕົວແທນຂອງສິ່ງນີ້. ພວກເຮົາສາມາດທົດສອບສົມຜົນນີ້ໂດຍການໃສ່ຄ່າງ່າຍໆ ສຳ ລັບ w. ຕົວຢ່າງ: ຖ້າສະ ໜາມ ກວ້າງ w = 10 ແມັດ, ມັນຈະຍາວ 10 + 30 = 40 ແມັດ. ຖ້າມັນກວ້າງ 30 ແມັດ, ມັນຈະມີຄວາມຍາວ 30 + 30 = 60 ແມັດ, ແລະອື່ນໆມັນເບິ່ງຄືວ່າມີເຫດຜົນ - ພວກເຮົາຄາດຫວັງວ່າພື້ນທີ່ຈະຍາວກວ່າເມື່ອມັນກວ້າງ, ສະນັ້ນສົມຜົນນີ້ເບິ່ງຄືວ່າເປັນການແກ້ໄຂທີ່ສົມເຫດສົມຜົນ.
3. ຈົ່ງຈື່ໄວ້ວ່າ ຄຳ ຕອບບໍ່ແມ່ນເລກເຕັມໃນເລກຄະນິດສາດ. ຄຳ ຕອບກ່ຽວກັບພຶດຊະຄະນິດແລະຄະນິດສາດອື່ນໆແມ່ນບໍ່ໄດ້ຕະຫຼອດ, ຕົວເລກງ່າຍ. ພວກມັນມັກຈະເປັນອັດຕານິຍົມ, ສ່ວນ ໜຶ່ງ ຫຼືຕົວເລກທີ່ບໍ່ສົມເຫດສົມຜົນ. ເຄື່ອງຄິດໄລ່ສາມາດຊ່ວຍທ່ານຊອກຫາ ຄຳ ຕອບທີ່ສັບສົນເຫລົ່ານີ້, ແຕ່ຈື່ໄວ້ວ່າຄູຂອງທ່ານອາດຈະຮ້ອງຂໍໃຫ້ທ່ານໃຫ້ ຄຳ ຕອບຢ່າງແນ່ນອນ, ບໍ່ແມ່ນສະຖານທີ່ທົດສະນິຍົມທີ່ບໍ່ເປັນລະບຽບ.
   • ຍົກຕົວຢ່າງ, ສົມມຸດວ່າພວກເຮົາໄດ້ຫຼຸດຜ່ອນສົມຜົນພຶດຊະຄະນິດມາເປັນ x = 1250. ຖ້າພວກເຮົາເຂົ້າ 1250 ເຂົ້າໃນເຄື່ອງຄິດໄລ່, ພວກເຮົາຈະໄດ້ຮັບສະຖານທີ່ອັດຕານິຍົມເປັນ ຈຳ ນວນຫລາຍ (ເພາະວ່າ ໜ້າ ຈໍຂອງເຄື່ອງຄິດໄລ່ມີພື້ນທີ່ ຈຳ ກັດ, ມັນບໍ່ສາມາດສະແດງ ຄຳ ຕອບເຕັມ). ໃນກໍລະນີນີ້, ພວກເຮົາພຽງແຕ່ສາມາດສະແດງ ຄຳ ຕອບໃຫ້ເປັນ 1250 ຫຼືງ່າຍດາຍ ຄຳ ຕອບໂດຍການຂຽນມັນໃສ່ໃນແນວຄິດວິທະຍາສາດ.
4. ຖ້າທ່ານຄຸ້ນເຄີຍກັບພື້ນຖານຂອງພຶດຊະຄະນິດ, ລອງປັດໃຈ. ໜຶ່ງ ໃນທັກສະທີ່ຫຍຸ້ງຍາກໃນການຄົ້ນຄວ້າກ່ຽວກັບພຶດຊະຄະນິດແມ່ນການຈັດປັດໄຈ - ການຕັດທາງລັດ ສຳ ລັບການຂຽນສົມຜົນທີ່ຊັບຊ້ອນໃນຮູບແບບທີ່ລຽບງ່າຍ. ປັດໃຈແມ່ນຫົວຂໍ້ທີ່ກ້າວ ໜ້າ ພໍສົມຄວນໃນຄະນິດສາດ, ສະນັ້ນເບິ່ງບົດຂຽນທີ່ເຊື່ອມໂຍງຂ້າງເທິງຖ້າທ່ານເຫັນວ່າມັນເປັນຫົວຂໍ້ທີ່ຍາກ. ຂ້າງລຸ່ມນີ້ແມ່ນ ຄຳ ແນະ ນຳ ບາງຢ່າງທີ່ຈະຊ່ວຍໃຫ້ທ່ານສາມາດໄຈ້ແຍກສົມຜົນ:
   • ສົມຜົນຂອງຮູບແບບຕັດທອນລາຍຈ່າຍ + ປັດໃຈ ba ເຂົ້າໄປໃນ (x + b). ຕົວຢ່າງ: 2x + 4 = 2 (x + 2)
   • ສົມຜົນຂອງຮູບແບບ ax + + b ປັດໄຈໄປຫາ cx ((a / c) x + (b / c)) ບ່ອນທີ່ c ແມ່ນຕົວເລກໃຫຍ່ທີ່ສຸດທີ່ ເໝາະ ສົມກັບ a ແລະ b. ຕົວຢ່າງ: 3y + 12y = 3y (y + 4)
   • ສົມຜົນຂອງຮູບແບບ x + bx + c ປັດໄຈໃສ່ (x + y) (x + z) ບ່ອນທີ່ y × z = c ແລະ yx + zx = bx. ຕົວຢ່າງ: x + 4x + 3 = (x + 3) (x + 1).
5. ຝຶກ, ຝຶກ, ຝຶກ! ຄວາມຄືບ ໜ້າ ໃນການຮຽນກ່ຽວກັບຄະນິດສາດ (ແລະສາຂາຄະນິດສາດອື່ນໆ) ຮຽກຮ້ອງໃຫ້ມີການເຮັດວຽກ ໜັກ ແລະການຄ້າງຫ້ອງຫຼາຍ. ຢ່າກັງວົນ - ໂດຍການເອົາໃຈໃສ່ໃນຫ້ອງຮຽນ, ເຮັດວຽກບ້ານທຸກຢ່າງ, ແລະຂໍຄວາມຊ່ວຍເຫຼືອຈາກຄູຫຼືນັກຮຽນຄົນອື່ນໆເມື່ອ ຈຳ ເປັນ, ໃນທີ່ສຸດພຶດຊະຄະນິດກໍ່ຈະກາຍເປັນລັກສະນະທີສອງ.
6. ຂໍໃຫ້ຄູອາຈານຂອງທ່ານຊ່ວຍທ່ານໃນຫົວຂໍ້ທີ່ຫຼອກລວງ. ຖ້າທ່ານຮູ້ວ່າມັນຍາກທີ່ຈະຮຽນເອກະສານ, ຢ່າກັງວົນ - ທ່ານບໍ່ ຈຳ ເປັນຕ້ອງຮຽນຮູ້ດ້ວຍຕົນເອງ. ນາຍຄູຂອງທ່ານແມ່ນຜູ້ ທຳ ອິດທີ່ຊ່ວຍທ່ານ ຄຳ ຖາມ. ຫລັງຈາກຮຽນແລ້ວ, ຂໍຄວາມຊ່ວຍເຫລືອຈາກຄູໃຫ້ເປັນຢ່າງສຸພາບ. ຄູອາຈານທີ່ດີແມ່ນປົກກະຕິແລ້ວຈະອະທິບາຍຫົວຂໍ້ອີກຄັ້ງ ໜຶ່ງ ເມື່ອທ່ານເຂົ້າມາຫາພວກເຂົາຫຼັງຈາກຮຽນ, ແລະອາດຈະສາມາດສະ ໜອງ ເອກະສານການປະຕິບັດເພີ່ມເຕີມໃຫ້ທ່ານ.
   • ຖ້າເຫດຜົນບາງຢ່າງທີ່ຄູຂອງທ່ານບໍ່ສາມາດຊ່ວຍທ່ານໄດ້, ໃຫ້ຖາມພວກເຂົາກ່ຽວກັບທາງເລືອກໃນການສອນຢູ່ໂຮງຮຽນ. ຫລາຍໂຮງຮຽນມີບາງຮູບແບບຂອງການຮຽນພິເສດທີ່ໃຫ້ທ່ານມີເວລາແລະຄວາມເອົາໃຈໃສ່ທີ່ທ່ານຕ້ອງການທີ່ຈະຮຽນເກັ່ງໃນພຶດຊະຄະນິດ. ຈົ່ງຈື່ໄວ້ວ່າການໃຊ້ການຊ່ວຍເຫຼືອທີ່ບໍ່ມີຄ່າໃຊ້ຈ່າຍນັ້ນບໍ່ແມ່ນສິ່ງທີ່ ໜ້າ ອາຍ - ມັນເປັນຕົວຊີ້ບອກວ່າທ່ານສະຫຼາດພໍທີ່ຈະແກ້ໄຂບັນຫາຂອງທ່ານ!

ພາກທີ 5 ຂອງ 5: ການ ສຳ ຫຼວດຫົວຂໍ້ທີ່ກ້າວ ໜ້າ

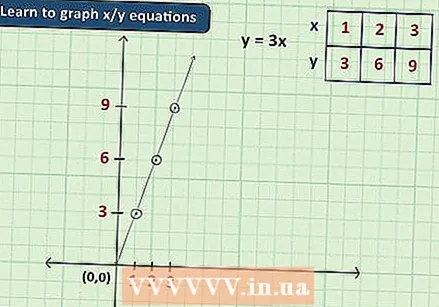1. ຮຽນຮູ້ວິທີການແຕ້ມເສັ້ນສົມຜົນ. ກາຟິກແມ່ນເຄື່ອງມືທີ່ມີຄຸນຄ່າໃນຄະນິດສາດເພາະວ່າມັນຊ່ວຍໃຫ້ທ່ານສາມາດເປັນຕົວແທນແນວຄວາມຄິດທີ່ມັກຈະຕ້ອງການຕົວເລກໃນຮູບພາບທີ່ເຂົ້າໃຈງ່າຍ. ໂດຍປົກກະຕິແລ້ວ, ເມື່ອເລີ່ມຕົ້ນດ້ວຍພຶດຊະຄະນິດ, ກາຟແມ່ນຖືກ ຈຳ ກັດສົມຜົນກັບສອງຕົວແປ (ປົກກະຕິ x ແລະ y) ແລະຖືກ ນຳ ສະ ເໜີ ໃນກາຟິກ 2-D ທີ່ງ່າຍດາຍດ້ວຍແກນ x ແລະແກນ y. ດ້ວຍສົມຜົນເຫຼົ່ານີ້, ສິ່ງທີ່ທ່ານຕ້ອງເຮັດແມ່ນໃສ່ຄ່າ ສຳ ລັບ x, ແລ້ວແກ້ ສຳ ລັບ y (ຫຼືໃນທາງກັບກັນ) ເພື່ອໃຫ້ໄດ້ສອງຕົວເລກທີ່ກົງກັບຈຸດທີ່ຢູ່ໃນເສັ້ນສະແດງ.
   • ຕົວຢ່າງ: ໃນສົມຜົນ y = 3x, ພວກເຮົາປ້ອນ 2 ສຳ ລັບ x, ແລະພວກເຮົາໄດ້ຮັບ y = 6 ເປັນ ຄຳ ຕອບ. ນີ້ຫມາຍຄວາມວ່າຈຸດ (2,6) (ສອງຈຸດຢູ່ເບື້ອງຂວາຂອງຈຸດສູນແລະ 6 ຂຶ້ນໄປ) ແມ່ນສ່ວນ ໜຶ່ງ ຂອງເສັ້ນສະແດງຂອງສົມຜົນ.
   • ສົມຜົນຂອງຮູບແບບ y = mx + b (ບ່ອນທີ່ m ແລະ b ແມ່ນຕົວເລກ) ພິເສດ ພຽງແຕ່ຢູ່ໃນພື້ນຖານຂອງພຶດຊະຄະນິດ. ສົມຜົນເຫຼົ່ານີ້ສະເຫມີມີຄ້ອຍ m ແລະຂ້າມແກນ y ຢູ່ຈຸດ y = b.
2. ຮຽນຮູ້ທີ່ຈະແກ້ໄຂຄວາມບໍ່ສະ ເໝີ ພາບ. ທ່ານຈະເຮັດແນວໃດເມື່ອສົມຜົນບໍ່ມີສັນຍານເທົ່າທຽມກັນ? ບໍ່ມີຫຍັງພິເສດເມື່ອທຽບໃສ່ກັບສິ່ງທີ່ທ່ານຈະເຮັດຖ້າບໍ່ດັ່ງນັ້ນ, ມັນຈະປ່ຽນໄປ. ສຳ ລັບຄວາມບໍ່ສະ ເໝີ ພາບ, ບ່ອນທີ່ທ່ານພົບກັບສັນຍານຕ່າງໆເຊັ່ນ, (("ໃຫຍ່ກວ່າ") ແລະ ("ນ້ອຍກວ່າ"), ແກ້ໄຂສົມຜົນໃນທາງດຽວກັນກັບຖ້າບໍ່ດັ່ງນັ້ນ. ຄຳ ຕອບທີ່ທ່ານໄດ້ຮັບແມ່ນນ້ອຍຫລືໃຫຍ່ກວ່າຕົວແປຂອງທ່ານ.
   • ຕົວຢ່າງ, ໃນສົມຜົນ 3> 5x - 2, ພວກເຮົາແກ້ໄຂມັນຄືກັນກັບສົມຜົນ ທຳ ມະດາ:

     3> 5 ເທົ່າ - 2

     5> 5 ເທົ່າ

     1> x, ຫຼື x 1.

   • ນີ້ ໝາຍ ຄວາມວ່າ ຕົວເລກນ້ອຍກວ່າ 1 ແມ່ນຖືກຕ້ອງ ສຳ ລັບ x. ໃນຄໍາສັບຕ່າງໆອື່ນໆ, x ສາມາດເປັນ 0, -1, -2, ແລະອື່ນໆ. ຖ້າພວກເຮົາໃສ່ຕົວເລກເຫລົ່ານີ້ເຂົ້າໄປໃນສົມຜົນ ສຳ ລັບ x, ພວກເຮົາຈະໄດ້ຮັບ ຄຳ ຕອບຕ່ ຳ ກວ່າ 3.
3. ແກ້ບັນຫາສີ່ຫລ່ຽມສີ່ຫລ່ຽມຫລືສີ່ຫລ່ຽມ. ຫົວຂໍ້ກ່ຽວກັບພຶດຊະຄະນິດທີ່ຫຼາຍຄົນເລີ່ມຕົ້ນສະດຸດລົງແມ່ນການແກ້ໄຂສົມຜົນສີ່ຫຼ່ຽມ. ນີ້ແມ່ນສົມຜົນຂອງຮູບແບບ ax + bx + c = 0, ບ່ອນທີ່ a, b ແລະ c ແມ່ນຕົວເລກ (ຍົກເວັ້ນບໍ່ສາມາດເປັນ 0). ພວກເຮົາແກ້ສົມຜົນເຫຼົ່ານີ້ດ້ວຍສູດ x = [- b +/- √ (b - 4ac)] / 2a. ຈົ່ງລະວັງ - +/- ໝາຍ ຄວາມວ່າທ່ານຕ້ອງໄດ້ຊອກຫາ ຄຳ ຕອບ ສຳ ລັບທັງສອງຢ່າງຕື່ມ ເປັນ ການຫັກລົບ, ດັ່ງນັ້ນສອງຄໍາຕອບແມ່ນເປັນໄປໄດ້ສໍາລັບປະເພດຂອງການອອກກໍາລັງກາຍເຫຼົ່ານີ້.
   • ຕົວຢ່າງ: ການແກ້ໄຂສູດສີ່ຫຼ່ຽມ 3x + 2x -1 = 0.

     x = [- b +/- √ (b - 4ac)] / 2a

     x = [- 2 +/- √ (2 - 4 (3) (- 1))] / 2 (3)

     x = [- 2 +/- √ (4 - (-12))] / 6

     x = [- 2 +/- √ (16)] / 6

     x = [- 2 +/- 4] / 6

     x =-1 ແລະ 1/3

4. ທົດລອງກັບລະບົບຂອງສົມຜົນ. ການແກ້ໄຂຫຼາຍສົມຜົນໃນເວລາດຽວກັນອາດຟັງຄືວ່າເປັນເລື່ອງຍາກ, ແຕ່ເມື່ອທ່ານເຮັດວຽກກັບສົມຜົນຄະນິດສາດທີ່ງ່າຍດາຍ, ມັນບໍ່ແມ່ນເລື່ອງຍາກເລີຍ. ຄູສອນຄະນິດສາດມັກໃຊ້ເສັ້ນສະແດງເພື່ອແກ້ໄຂບັນຫາເຫຼົ່ານີ້. ຖ້າທ່ານເຮັດວຽກກັບລະບົບຂອງສອງສະມະການ, ທ່ານຈະພົບເຫັນວິທີແກ້ໄຂໂດຍການເບິ່ງຈຸດຕ່າງໆໃນເສັ້ນສະແດງ, ບ່ອນທີ່ເສັ້ນຂອງເສັ້ນສະມະການທັງສອງຕັດກັນ.
   • ຕົວຢ່າງ: ສົມມຸດວ່າພວກເຮົາ ກຳ ລັງຈັດການກັບລະບົບຂອງສົມຜົນ y = 3x - 2 ແລະ y = -x - 6. ຖ້າພວກເຮົາແຕ້ມເສັ້ນສອງເສັ້ນນີ້ໃນເສັ້ນສະແດງ, ພວກເຮົາຈະໄດ້ເສັ້ນທີ່ຂື້ນຂື້ນສູງແລະເສັ້ນ ໜຶ່ງ ທີ່ໄປ ໜ້ອຍ ລົງ ລົງຢ່າງສູງ. ເນື່ອງຈາກວ່າສາຍເຫຼົ່ານີ້ຕັດກັນຢູ່ຈຸດ (-1,-5), ນັ້ນແມ່ນການແກ້ໄຂຂອງລະບົບ.
   • ເພື່ອກວດສອບສິ່ງນີ້, ລວມເອົາ ຄຳ ຕອບເຂົ້າໃນສົມຜົນຂອງລະບົບ - ຄຳ ຕອບທີ່ຖືກຕ້ອງຄວນ "ເຮັດວຽກ" ສຳ ລັບທັງສອງສົມຜົນ.

     y = 3 ເທົ່າ - 2

     -5=3(-1) - 2

     -5=-3 - 2

     -5=-5

     y = -x - 6

     -5=-(-1) - 6

     -5=1 - 6

     -5=-5

   • ສົມຜົນທັງສອງແມ່ນ "ຖືກຕ້ອງ", ສະນັ້ນ ຄຳ ຕອບຂອງພວກເຮົາແມ່ນຖືກຕ້ອງ!

ຄຳ ແນະ ນຳ

• ມີຊັບພະຍາກອນຫຼາຍໂຕນ ສຳ ລັບຄົນທີ່ຕ້ອງການຮຽນຮູ້ພຶດຊະຄະນິດອອນລາຍ. ພຽງແຕ່ການຄົ້ນຫາແບບງ່າຍໆໃນເຄື່ອງຈັກຊອກຫາຄ້າຍຄື "ການຊ່ວຍເຫລືອດ້ານພຶດຊະຄະນິດ" ສາມາດໃຫ້ຜົນໄດ້ຮັບທີ່ດີຫຼາຍສິບຢ່າງ. ຍັງກວດເບິ່ງປະເພດເລກຂອງ wikiHow. ຢູ່ທີ່ນັ້ນທ່ານຈະເຫັນຂໍ້ມູນຫຼາຍຢ່າງ, ສະນັ້ນເລີ່ມຕົ້ນທັນທີ!
• ເວັບໄຊທ໌ ໜຶ່ງ ທີ່ດີ ສຳ ລັບຜູ້ເລີ່ມຕົ້ນຄະນິດສາດແມ່ນ khanacademy.com. ເວບໄຊທ໌ຟຣີນີ້ມີບົດສະ ເໜີ ບົດຮຽນທີ່ງ່າຍຕໍ່ການຕິດຕາມຫຼາຍຫົວຂໍ້ລວມທັງພຶດຊະຄະນິດ. ມີວິດີໂອກ່ຽວກັບທຸກສິ່ງທຸກຢ່າງຈາກງ່າຍດາຍທີ່ສຸດເຖິງຫົວຂໍ້ລະດັບມະຫາວິທະຍາໄລ, ສະນັ້ນຢ່າລັງເລທີ່ຈະໃຊ້ປະໂຫຍດຈາກ Khan Academy ແລະທຸກໆການຊ່ວຍເຫຼືອໃນເວັບໄຊທ໌ນີ້ສາມາດໃຫ້ທ່ານໄດ້!
• ຈື່ໄວ້ວ່າຊັບພະຍາກອນທີ່ດີທີ່ສຸດ ສຳ ລັບການຮຽນຄະນິດສາດແມ່ນຄົນທີ່ທ່ານຮູ້ຈັກແລ້ວ. ປຶກສາກັບ ໝູ່ ເພື່ອນຫຼືນັກຮຽນຄົນອື່ນໆທີ່ເຂົ້າຮຽນໃນຫ້ອງດຽວກັນຖ້າທ່ານຕ້ອງການຄວາມຊ່ວຍເຫຼືອກ່ຽວກັບຫົວຂໍ້ທີ່ຂຽນໄວ້ໃນຫ້ອງຮຽນ.