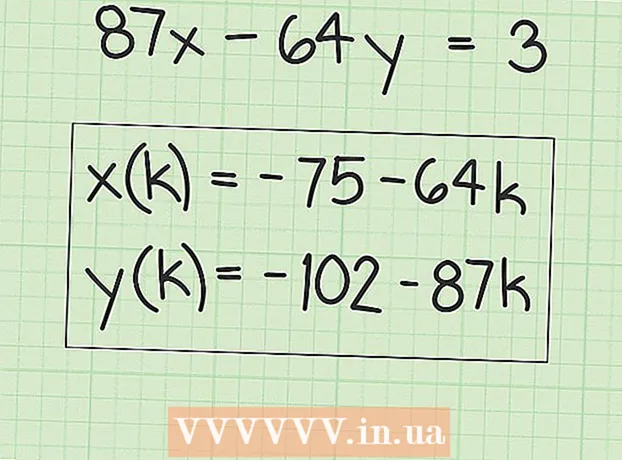
ເນື້ອຫາ

• ຂັ້ນຕອນ
• ສ່ວນທີ 1 ຂອງ 4: ວິທີການຂຽນສົມຜົນ
• ສ່ວນທີ 2 ຂອງ 4: ວິທີການຂຽນສູດການຄິດໄລ່ຂອງ Euclid
• ສ່ວນທີ 3 ຂອງ 4: ວິທີຊອກຫາວິທີແກ້ໄຂບັນຫາໂດຍໃຊ້ Algorithm ຂອງ Euclid
• ສ່ວນທີ 4 ຂອງ 4: ຊອກຫາວິທີແກ້ໄຂບັນຫາອື່ນinທີ່ບໍ່ມີຂອບເຂດ

ເພື່ອແກ້ໄຂສົມຜົນ Diophantine ເສັ້ນຊື່, ເຈົ້າຕ້ອງການຊອກຫາຄ່າຂອງຕົວແປ "x" ແລະ "y", ເຊິ່ງເປັນຈໍານວນເຕັມ. ການແກ້ໄຂເລກເຕັມມີຄວາມຊັບຊ້ອນຫຼາຍກວ່າປົກກະຕິແລະຮຽກຮ້ອງໃຫ້ມີການກະ ທຳ ສະເພາະ. ທຳ ອິດ, ເຈົ້າຕ້ອງການຄິດໄລ່ຕົວຫານຕົວຄູນ ທຳ ມະດາທີ່ສຸດ (GCD), ແລະຈາກນັ້ນຊອກຫາທາງອອກ. ເມື່ອເຈົ້າໄດ້ພົບເຫັນການແກ້ໄຂບັນຫາຈໍານວນເຕັມອັນນຶ່ງໃສ່ສົມຜົນເສັ້ນຊື່, ເຈົ້າສາມາດໃຊ້ຮູບແບບງ່າຍ simple ເພື່ອຊອກຫາຈໍານວນທາງອອກທີ່ບໍ່ຈໍາກັດຈໍານວນນຶ່ງ.

ຂັ້ນຕອນ

ສ່ວນທີ 1 ຂອງ 4: ວິທີການຂຽນສົມຜົນ

1. 1 ຂຽນສົມຜົນລົງໃນຮູບແບບມາດຕະຖານ. ສົມຜົນເສັ້ນຊື່ເປັນສົມຜົນທີ່ຕົວຊີ້ວັດຂອງຕົວແປບໍ່ເກີນ 1. ເພື່ອແກ້ໄຂສົມຜົນເສັ້ນຊື່ດັ່ງກ່າວ, ທຳ ອິດໃຫ້ຂຽນມັນໃນຮູບແບບມາດຕະຖານ. ຮູບແບບມາດຕະຖານຂອງສົມຜົນເສັ້ນຊື່ຄ້າຍຄືນີ້: ${ displaystyle Ax + ໂດຍ = C}$, ບ່ອນທີ່ ${ displaystyle A, B}$ ແລະ ${ displaystyle C}$ - ຕົວເລກທັງຫມົດ.
   • ຖ້າສົມຜົນຖືກມອບໃຫ້ໃນຮູບແບບທີ່ແຕກຕ່າງ, ນຳ ມັນມາສູ່ຮູບແບບມາດຕະຖານໂດຍ ນຳ ໃຊ້ການປະຕິບັດພຶດຊະຄະນິດພື້ນຖານ. ຕົວຢ່າງ, ໃຫ້ສົມຜົນ ${ displaystyle 23x + 4y -7x = -3y + 15}$... ໃຫ້ ຄຳ ສັບຄ້າຍຄືກັນແລະຂຽນສົມຜົນຄືແນວນີ້: ${ displaystyle 16x + 7y = 15}$.
2. 2 ເຮັດໃຫ້ສົມຜົນງ່າຍຂຶ້ນ (ຖ້າເປັນໄປໄດ້). ເມື່ອເຈົ້າຂຽນສົມຜົນໃນຮູບແບບມາດຕະຖານ, ເບິ່ງຕົວຄູນ ${ displaystyle A, B}$ ແລະ ${ displaystyle C}$... ຖ້າອັດຕາຄີກເຫຼົ່ານີ້ມີ GCD, ຈົ່ງແບ່ງໂອກາດທັງສາມໂດຍມັນ. ການແກ້ໄຂບັນຫາສົມຜົນທີ່ລຽບງ່າຍນັ້ນຍັງຈະເປັນການແກ້ໄຂບັນຫາສົມຜົນເດີມ.
   • ຕົວຢ່າງ, ຖ້າຜົນຄູນສາມທັງareົດເທົ່າກັນ, ຫານພວກມັນຢ່າງ ໜ້ອຍ 2. ຕົວຢ່າງ:
     • ${ displaystyle 42x + 36y = 48}$ (ສະມາຊິກທັງareົດແບ່ງອອກເປັນ 2)
     • ${ displaystyle 21x + 18y = 24}$ (ຕອນນີ້ສະມາຊິກທັງareົດແບ່ງອອກເປັນ 3)
     • ${ displaystyle 7x + 6y = 8}$ (ສົມຜົນນີ້ບໍ່ສາມາດເຮັດໃຫ້ງ່າຍຂຶ້ນໄດ້ອີກຕໍ່ໄປ)
3. 3 ກວດເບິ່ງວ່າສົມຜົນສາມາດແກ້ໄຂໄດ້. ໃນບາງກໍລະນີ, ເຈົ້າສາມາດບອກໄດ້ທັນທີວ່າສົມຜົນບໍ່ມີທາງອອກ. ຖ້າຕົວຄູນ "C" ບໍ່ສາມາດຫານໄດ້ໂດຍ GCD ຂອງຕົວຄູນ "A" ແລະ "B", ສົມຜົນບໍ່ມີທາງອອກ.
   • ຕົວຢ່າງ, ຖ້າທັງສອງຕົວຄູນ ${ displaystyle A}$ ແລະ ${ displaystyle B}$ ແມ່ນເທົ່າກັນ, ຫຼັງຈາກນັ້ນຕົວຄູນ ${ displaystyle C}$ ຕ້ອງເທົ່າກັນ. ແຕ່ຖ້າ ${ displaystyle C}$ ຄີກ, ຫຼັງຈາກນັ້ນບໍ່ມີການແກ້ໄຂ.
     • ສົມຜົນ ${ displaystyle 2x + 4y = 21}$ ບໍ່ມີການແກ້ໄຂເລກເຕັມ.
     • ສົມຜົນ ${ displaystyle 5x + 10y = 17}$ ບໍ່ມີການແກ້ໄຂເລກເຕັມນັບຕັ້ງແຕ່ເບື້ອງຊ້າຍຂອງສົມຜົນແມ່ນສາມາດຫານໄດ້ດ້ວຍ 5 ແລະດ້ານຂວາບໍ່ແມ່ນ.

ສ່ວນທີ 2 ຂອງ 4: ວິທີການຂຽນສູດການຄິດໄລ່ຂອງ Euclid

1. 1 ເຂົ້າໃຈສູດການຄິດໄລ່ຂອງ Euclid. ມັນແມ່ນຊຸດຂອງການແບ່ງແຍກຊ້ ຳ in ທີ່ຕົວທີ່ເຫຼືອກ່ອນ ໜ້າ ນີ້ຖືກໃຊ້ເປັນຕົວຫານຖັດໄປ. ຕົວຫານສຸດທ້າຍທີ່ຫານຕົວເລກອອກເປັນສ່ວນ is ແມ່ນຕົວຫານທົ່ວໄປທີ່ໃຫຍ່ທີ່ສຸດ (GCD) ຂອງສອງຕົວເລກ.
   • ຕົວຢ່າງ, ໃຫ້ຊອກຫາ GCD ຂອງຕົວເລກ 272 ແລະ 36 ໂດຍໃຊ້ວິທີການຄິດໄລ່ຂອງ Euclid:
     • ${ displaystyle 272 = 7 * 36 + 20}$ - ຫານຕົວເລກໃຫຍ່ (272) ໂດຍຕົວເລກທີ່ນ້ອຍກວ່າ (36) ແລະເອົາໃຈໃສ່ສ່ວນທີ່ເຫຼືອ (20);
     • ${ displaystyle ຮູບແບບ 36 = 1 * 20 + 16}$ - ຫານຕົວຫານກ່ອນ ໜ້າ (36) ດ້ວຍຈໍານວນທີ່ເຫຼືອກ່ອນ ໜ້າ (20). Noteາຍເຫດສານຕົກຄ້າງໃ(່ (16);
     • ${ displaystyle 20 = 1 * 16 + 4}$ - ຫານຕົວຫານກ່ອນ ໜ້າ (20) ດ້ວຍ ຈຳ ນວນທີ່ເຫຼືອກ່ອນ ໜ້າ (16). Noteາຍເຫດສານຕົກຄ້າງໃ(່ (4);
     • ${ displaystyle 16 = 4 * 4 + 0}$ - ຫານຕົວຫານກ່ອນ ໜ້າ (16) ດ້ວຍຈໍານວນທີ່ເຫຼືອກ່ອນ ໜ້າ (4). ເນື່ອງຈາກສ່ວນທີ່ເຫຼືອແມ່ນ 0, ພວກເຮົາສາມາດເວົ້າໄດ້ວ່າ 4 ແມ່ນ GCD ຂອງສອງຕົວເລກເດີມ 272 ແລະ 36.
2. 2 ນຳ ໃຊ້ສູດການຄິດໄລ່ຂອງ Euclid ກັບຕົວຄູນ "A" ແລະ "B". ເມື່ອເຈົ້າຂຽນສົມຜົນເສັ້ນຊື່ໃນຮູບແບບມາດຕະຖານ, ກໍານົດຄ່າສໍາປະສິດ "A" ແລະ "B" ແລະຈາກນັ້ນນໍາໃຊ້ວິທີການຄິດໄລ່ຂອງ Euclid ໃຫ້ເຂົາເຈົ້າຊອກຫາ GCD. ຕົວຢ່າງ, ໃຫ້ສົມຜົນເສັ້ນຊື່ ${ displaystyle 87x-64y = 3}$.
   • ນີ້ແມ່ນສູດການຄິດໄລ່ຂອງ Euclid ສໍາລັບຕົວຄູນ A = 87 ແລະ B = 64:
     • ${ displaystyle 87 = 1 * 64 + 23}$
     • ${ displaystyle 64 = 2 * 23 + 18}$
     • ${ displaystyle 23 = 1 * 18 + 5}$
     • ${ displaystyle 18 = 3 * 5 + 3}$
     • ${ displaystyle 5 = 1 * 3 + 2}$
     • ${ displaystyle 3 = 1 * 2 + 1}$
     • ${ displaystyle 2 = 2 * 1 + 0}$
3. 3 ຊອກຫາປັດໃຈສາມັນທີ່ຍິ່ງໃຫຍ່ທີ່ສຸດ (GCD). ເນື່ອງຈາກຕົວຫານສຸດທ້າຍແມ່ນ 1, GCD 87 ແລະ 64 ແມ່ນ 1. ດັ່ງນັ້ນ, 87 ແລະ 64 ແມ່ນຕົວເລກຕົ້ນຕໍທີ່ກ່ຽວຂ້ອງກັບກັນແລະກັນ.
4. 4 ວິເຄາະຜົນໄດ້ຮັບ. ເມື່ອເຈົ້າພົບຕົວຄູນ gcd ${ displaystyle A}$ ແລະ ${ displaystyle B}$, ສົມທຽບມັນກັບຕົວຄູນ ${ displaystyle C}$ ສົມຜົນເດີມ. ຖ້າ ${ displaystyle C}$ ແບ່ງອອກໂດຍ gcd ${ displaystyle A}$ ແລະ ${ displaystyle B}$, ສົມຜົນມີການແກ້ໄຂເລກເຕັມ; ຖ້າບໍ່ດັ່ງນັ້ນສົມຜົນບໍ່ມີທາງອອກ.
   • ຕົວຢ່າງ, ສົມຜົນ ${ displaystyle 87x-64y = 3}$ ສາມາດແກ້ໄຂໄດ້ເພາະວ່າ 3 ສາມາດຫານໄດ້ດ້ວຍ 1 (gcd = 1).
   • ຕົວຢ່າງ, ສົມມຸດວ່າ GCD = 5. 3 ບໍ່ສາມາດຫານດ້ວຍ 5 ໄດ້ສະເີ, ດັ່ງນັ້ນສົມຜົນນີ້ຈຶ່ງບໍ່ມີວິທີແກ້ເລກເຕັມ.
   • ດັ່ງທີ່ສະແດງຢູ່ຂ້າງລຸ່ມ, ຖ້າສົມຜົນມີການແກ້ໄຂເລກເຕັມຈໍານວນ ໜຶ່ງ, ມັນຍັງມີຈໍານວນບໍ່ຈໍາກັດຂອງການແກ້ໄຂບັນຫາຈໍານວນເຕັມອື່ນ.

ສ່ວນທີ 3 ຂອງ 4: ວິທີຊອກຫາວິທີແກ້ໄຂບັນຫາໂດຍໃຊ້ Algorithm ຂອງ Euclid

1. 1 ຈໍານວນຂັ້ນຕອນສໍາລັບການຄິດໄລ່ GCD. ເພື່ອຊອກຫາວິທີແກ້ໄຂບັນຫາສົມຜົນເສັ້ນຊື່, ເຈົ້າຕ້ອງໃຊ້ວິທີການຄິດໄລ່ Euclidean ເປັນພື້ນຖານສໍາລັບການທົດແທນແລະຂະບວນການເຮັດໃຫ້ງ່າຍຂຶ້ນ.
   • ເລີ່ມດ້ວຍການນັບຈໍານວນຂັ້ນຕອນສໍາລັບການຄິດໄລ່ GCD. ຂະບວນການຄິດໄລ່ຄືແນວນີ້:
     • ${ displaystyle { text {ຂັ້ນຕອນທີ 1}}: 87 = (1 * 64) +23}$
     • ${ displaystyle { text {ຂັ້ນຕອນທີ 2}}: 64 = (2 * 23) +18}$
     • ${ displaystyle { text {ຂັ້ນຕອນທີ 3}}: 23 = (1 * 18) +5}$
     • ${ displaystyle { text {ຂັ້ນຕອນທີ 4}}: 18 = (3 * 5) +3}$
     • ${ displaystyle { text {ຂັ້ນຕອນທີ 5}}: 5 = (1 * 3) +2}$
     • ${ displaystyle { text {ຂັ້ນຕອນ 6}}: 3 = (1 * 2) +1}$
     • ${ displaystyle { text {ຂັ້ນຕອນທີ 7}}: 2 = (2 * 1) +0}$
2. 2 ເອົາໃຈໃສ່ກັບຂັ້ນຕອນສຸດທ້າຍ, ບ່ອນທີ່ຍັງເຫຼືອ. ຂຽນສົມຜົນຄືນໃstep່ ສຳ ລັບຂັ້ນຕອນນີ້ເພື່ອແຍກສ່ວນທີ່ເຫຼືອ.
   • ໃນຕົວຢ່າງຂອງພວກເຮົາ, ຂັ້ນຕອນສຸດທ້າຍທີ່ເຫຼືອແມ່ນຂັ້ນຕອນທີ 6. ສ່ວນທີ່ເຫຼືອແມ່ນ 1. ຂຽນສົມຜົນຄືນໃin່ໃນຂັ້ນຕອນທີ 6 ດັ່ງຕໍ່ໄປນີ້:
     • ${ displaystyle 1 = 3- (1 * 2)}$
3. 3 ແຍກສ່ວນທີ່ເຫຼືອຂອງຂັ້ນຕອນກ່ອນ ໜ້າ. ຂະບວນການນີ້ແມ່ນເປັນຂັ້ນຕອນ "ຍ້າຍຂຶ້ນ". ແຕ່ລະຄັ້ງເຈົ້າຈະແຍກສ່ວນທີ່ເຫຼືອຢູ່ໃນສົມຜົນໃນຂັ້ນຕອນກ່ອນ ໜ້າ.
   • ແຍກສ່ວນທີ່ຍັງເຫຼືອຂອງສົມຜົນໃນຂັ້ນຕອນທີ 5:
     • ${ displaystyle 2 = 5- (1 * 3)}$ ຫຼື ${ displaystyle 2 = 5-3}$
4. 4 ທົດແທນແລະເຮັດໃຫ້ງ່າຍຂຶ້ນ. ສັງເກດເຫັນວ່າສົມຜົນໃນຂັ້ນຕອນ 6 ປະກອບມີຕົວເລກ 2, ແລະໃນສົມຜົນໃນຂັ້ນຕອນທີ 5, ຕົວເລກ 2 ແມ່ນແຍກອອກຈາກກັນ. ສະນັ້ນແທນທີ່ຈະເປັນ“ 2” ໃນສົມຜົນໃນຂັ້ນຕອນທີ 6, ແທນການສະແດງອອກໃນຂັ້ນຕອນທີ 5:
   • ${ displaystyle 1 = 3-2}$ (ສົມຜົນຂອງຂັ້ນຕອນ 6)
   • ${ displaystyle 1 = 3- (5-3)}$ (ແທນທີ່ 2, ການສະແດງອອກໄດ້ຖືກແທນທີ່)
   • ${ displaystyle 1 = 3-5 + 3}$ (ວົງເລັບເປີດ)
   • ${ displaystyle 1 = 2 (3) -5}$ (ແບບງ່າຍ)
5. 5 ເຮັດຊ້ ຳ ການທົດແທນແລະຂະບວນການເຮັດໃຫ້ລຽບງ່າຍ. ເຮັດຊ້ ຳ ຂະບວນການທີ່ໄດ້ອະທິບາຍໄວ້, ເຄື່ອນຍ້າຍຜ່ານລະບົບ Euclidean ໃນ ລຳ ດັບປີ້ນກັບກັນ. ແຕ່ລະຄັ້ງເຈົ້າຈະຂຽນສົມຜົນຄືນໃstep່ຈາກຂັ້ນຕອນກ່ອນ ໜ້າ ແລະສຽບມັນໃສ່ສົມຜົນສຸດທ້າຍທີ່ເຈົ້າໄດ້ຮັບ.
   • ຂັ້ນຕອນສຸດທ້າຍທີ່ພວກເຮົາເບິ່ງແມ່ນຂັ້ນຕອນ 5. ດັ່ງນັ້ນ, ໄປຫາຂັ້ນຕອນ 4 ແລະແຍກສ່ວນທີ່ເຫຼືອຢູ່ໃນສົມຜົນສໍາລັບຂັ້ນຕອນນັ້ນ:
     • ${ displaystyle 3 = 18- (3 * 5)}$
   • ແທນການສະແດງອອກນີ້ສໍາລັບ "3" ໃນສົມຜົນສຸດທ້າຍ:
     • ${ displaystyle 1 = 2 (18-3 * 5) -5}$
     • ${ displaystyle 1 = 2 (18) -6 (5) -5}$
     • ${ displaystyle 1 = 2 (18) -7 (5)}$
6. 6 ສືບຕໍ່ດ້ວຍການທົດແທນແລະຂະບວນການເຮັດໃຫ້ລຽບງ່າຍ. ຂັ້ນຕອນນີ້ຈະຖືກເຮັດຊ້ ຳ ອີກຈົນກວ່າເຈົ້າຈະໄປຮອດຂັ້ນຕອນເບື້ອງຕົ້ນຂອງການຄິດໄລ່ Euclidean. ເປົ້າofາຍຂອງຂະບວນການແມ່ນຂຽນສົມຜົນດ້ວຍຕົວຄູນ 87 ແລະ 64 ຂອງສົມຜົນເດີມທີ່ຈະແກ້ໄຂ. ໃນຕົວຢ່າງຂອງພວກເຮົາ:
   • ${ displaystyle 1 = 2 (18) -7 (5)}$
   • ${ displaystyle 1 = 2 (18) -7 (23-18)}$ (ແທນການສະແດງອອກຈາກຂັ້ນຕອນ 3)
     • ${ displaystyle 1 = 2 (18) -7 (23) +7 (18)}$
     • ${ displaystyle 1 = 9 (18) -7 (23)}$
   • ${ displaystyle 1 = 9 (64-2 * 23) -7 (23)}$ (ແທນການສະແດງອອກຈາກຂັ້ນຕອນ 2)
     • ${ displaystyle 1 = 9 (64) -18 (23) -7 (23)}$
     • ${ displaystyle 1 = 9 (64) -25 (23)}$
   • ${ displaystyle 1 = 9 (64) -25 (87-64)}$ (ແທນການສະແດງອອກຈາກຂັ້ນຕອນ 1)
     • ${ displaystyle 1 = 9 (64) -25 (87) +25 (64)}$
     • ${ displaystyle 1 = 34 (64) -25 (87)}$
7. 7 ຂຽນສົມຜົນທີ່ໄດ້ຮັບຄືນໃin່ໃຫ້ສອດຄ່ອງກັບຕົວຄູນເດີມ. ເມື່ອເຈົ້າກັບຄືນສູ່ຂັ້ນຕອນທໍາອິດຂອງສູດຄິດໄລ່ Euclidean, ເຈົ້າຈະເຫັນວ່າສົມຜົນທີ່ໄດ້ຮັບມີສອງຕົວຄູນຂອງສົມຜົນເດີມ. ຂຽນສົມຜົນຄືນໃso່ເພື່ອໃຫ້ ລຳ ດັບຂອງຂໍ້ກໍານົດຂອງມັນກົງກັບຕົວຄູນຂອງສົມຜົນເດີມ.
   • ໃນຕົວຢ່າງຂອງພວກເຮົາ, ສົມຜົນເດີມ ${ displaystyle 87x-64y = 3}$... ດັ່ງນັ້ນ, ຂຽນສົມຜົນທີ່ໄດ້ຮັບຄືນໃso່ເພື່ອໃຫ້ຕົວຄູນຖືກນໍາມາເປັນແຖວ.ເອົາໃຈໃສ່ເປັນພິເສດຕໍ່ຕົວຄູນ“ 64”. ໃນສົມຜົນເດີມ, ຕົວຄູນນີ້ເປັນລົບ, ແລະໃນສູດການຄິດໄລ່ Euclidean, ມັນເປັນບວກ. ດັ່ງນັ້ນ, ປັດໃຈ 34 ຕ້ອງໄດ້ເຮັດໃຫ້ເປັນລົບ. ສົມຜົນສຸດທ້າຍຈະຖືກຂຽນໄວ້ດັ່ງນີ້:
     • ${ displaystyle 87 (-25) -64 (-34) = 1}$
8. 8 ນຳ ໃຊ້ຕົວຄູນທີ່ເາະສົມເພື່ອຊອກຫາທາງອອກ. ຈື່ໄວ້ວ່າໃນຕົວຢ່າງຂອງພວກເຮົາ, GCD = 1, ສະນັ້ນສົມຜົນສຸດທ້າຍແມ່ນ 1. ແຕ່ສົມຜົນເດີມ (87x-64y) ແມ່ນ 3. ດັ່ງນັ້ນ, ທຸກເງື່ອນໄຂໃນສົມຜົນສຸດທ້າຍຕ້ອງໄດ້ຄູນດ້ວຍ 3 ເພື່ອໃຫ້ໄດ້ຄໍາຕອບ:
   • ${ displaystyle 87 (-25 * 3) -64 (-34 * 3) = 1 * 3}$
   • ${ displaystyle 87 (-75) -64 (-102) = 3}$
9. 9 ຂຽນຕົວແກ້ເລກເຕັມໃສ່ສົມຜົນ. ຕົວເລກທີ່ຄູນດ້ວຍຕົວຄູນຂອງສົມຜົນເດີມແມ່ນການແກ້ໄຂບັນຫາສົມຜົນນັ້ນ.
   • ໃນຕົວຢ່າງຂອງພວກເຮົາ, ຂຽນການແກ້ໄຂເປັນຄູ່ພິກັດ: ${ displaystyle (x, y) = ( - 75, -102)}$.

ສ່ວນທີ 4 ຂອງ 4: ຊອກຫາວິທີແກ້ໄຂບັນຫາອື່ນinທີ່ບໍ່ມີຂອບເຂດ

1. 1 ເຂົ້າໃຈວ່າມີຈໍານວນຈໍານວນບໍ່ຈໍາກັດຂອງການແກ້ໄຂ. ຖ້າສົມຜົນເສັ້ນຊື່ມີຕົວແກ້ເລກເຕັມ ຈຳ ນວນ ໜຶ່ງ, ຫຼັງຈາກນັ້ນມັນຈະຕ້ອງມີການແກ້ໄຂບັນຫາ ຈຳ ນວນເຕັມ ຈຳ ນວນບໍ່ມີຂອບເຂດ. ນີ້ແມ່ນຫຼັກຖານໄວ (ໃນຮູບແບບພຶດຊະຄະນິດ):
   • ${ displaystyle Ax + ໂດຍ = C}$
   • ${ displaystyle A (x + B) + B (y-A) = C}$ (ຖ້າເຈົ້າເພີ່ມ "B" ໃສ່ "x" ແລະລົບ "A" ອອກຈາກ "y", ຄ່າຂອງສົມຜົນເດີມຈະບໍ່ປ່ຽນແປງ)
2. 2 ບັນທຶກຄ່າຕົ້ນສະບັບ x ແລະ y. ແມ່ແບບ ສຳ ລັບຄິດໄລ່ການແກ້ໄຂບັນຫາຕໍ່ໄປ (ບໍ່ມີຂອບເຂດ) ເລີ່ມຕົ້ນດ້ວຍວິທີແກ້ໄຂອັນດຽວທີ່ເຈົ້າໄດ້ພົບມາແລ້ວ.
   • ໃນຕົວຢ່າງຂອງພວກເຮົາ, ການແກ້ໄຂແມ່ນຄູ່ຂອງພິກັດ ${ displaystyle (x, y) = ( - 75, -102)}$.
3. 3 ເພີ່ມປັດໃຈ "B" ໃສ່ຄ່າ "x". ເຮັດອັນນີ້ເພື່ອຊອກຫາຄ່າ x ໃnew່.
   • ໃນຕົວຢ່າງຂອງພວກເຮົາ, x = -75, ແລະ B = -64:
     • ${ displaystyle x = -75 + ( - 64) = - 139}$
   • ດັ່ງນັ້ນ, ຄ່າໃ"່ "x": x = -139.
4. 4 ລົບປັດໃຈ "A" ອອກຈາກຄ່າ "y". ເພື່ອວ່າມູນຄ່າຂອງສົມຜົນເດີມບໍ່ປ່ຽນແປງ, ເມື່ອເພີ່ມຕົວເລກ ໜຶ່ງ ໃສ່ "x", ເຈົ້າຕ້ອງການລົບເລກອື່ນອອກຈາກ "y".
   • ໃນຕົວຢ່າງຂອງພວກເຮົາ, y = -102, ແລະ A = 87:
     • ${ displaystyle y = -102-87 = -189}$
   • ດັ່ງນັ້ນ, ຄ່າໃfor່ ສຳ ລັບ "y": y = -189.
   • ຄູ່ພິກັດຄູ່ໃwill່ຈະຖືກຂຽນດັ່ງນີ້: ${ displaystyle (x, y) = ( - 139, -189)}$.
5. 5 ກວດເບິ່ງການແກ້ໄຂ. ເພື່ອກວດພິສູດວ່າຄູ່ປະສານງານໃis່ເປັນການແກ້ໄຂສົມຜົນເດີມ, ສຽບຄ່າເຂົ້າໄປໃນສົມຜົນ.
   • ${ displaystyle 87x-64y = 3}$
   • ${ displaystyle 87 (-139) -64 (-189) = 3}$
   • ${ displaystyle 3 = 3}$
   • ເນື່ອງຈາກຄວາມສະເີພາບບັນລຸໄດ້, ການຕັດສິນໃຈແມ່ນຖືກຕ້ອງ.
6. 6 ຂຽນ ສຳ ນວນລົງເພື່ອຊອກຫາວິທີແກ້ໄຂຫຼາຍບັນຫາ. ຄ່າ "x" ຈະເທົ່າກັບການແກ້ໄຂຕົ້ນສະບັບບວກກັບຕົວຄູນໃດ B ຂອງ "B". ອັນນີ້ສາມາດຂຽນເປັນ ສຳ ນວນຕໍ່ໄປນີ້ໄດ້:
   • x (k) = x + k (B), ບ່ອນທີ່“ x (k)” ແມ່ນຊຸດຂອງ“ x” ຄ່າແລະ“ x” ແມ່ນຄ່າເດີມ (ທໍາອິດ) ຂອງ“ x” ທີ່ເຈົ້າພົບເຫັນ.
     • ໃນຕົວຢ່າງຂອງພວກເຮົາ:
     • ${ displaystyle x (k) = - 75-64k}$
   • y (k) = y-k (A), ບ່ອນທີ່ y (k) ແມ່ນຊຸດຂອງຄ່າ y ແລະ y ແມ່ນຄ່າເດີມ (ທໍາອິດ) y ທີ່ເຈົ້າພົບເຫັນ.
     • ໃນຕົວຢ່າງຂອງພວກເຮົາ:
     • ${ displaystyle y (k) = - 102-87k}$